こんにちは！ケントです！
中1「文字と式」の最初の内容です。
中学校の数学では、\(a,b,x,y,z\)などの
文字を使って式を作ったり、方程式を解いたり
とにかく文字を使って考えることが多くなります。
これまでは
実際の数をで計算することが多かったので
いきなり文字と聞くと
拒絶反応を示してしまう子もいると思います。
でも大丈夫、それが普通です！
自分もそうでした。
なんで数学なのに文字使う必要があるの？って感じ…
でも、数学の勉強を進むと気づくんですね。
文字で考えることの大切さや必要さに。
それは勉強を進めながら感じてくれたらいいので
今は「必要なものなんだ」となんとか踏ん張って下さい！
文字を使った式
「なんで文字を使う必要があるの？」
という思う子がたくさんいると思います。
まずは、数学で文字を使うとこんなに便利なんだよ！
ということを知ってもらおうと思います！
下の図のようにマッチ棒を規則的に並べていくことを考えましょう。
それぞれの状態を①〜⑤としました。
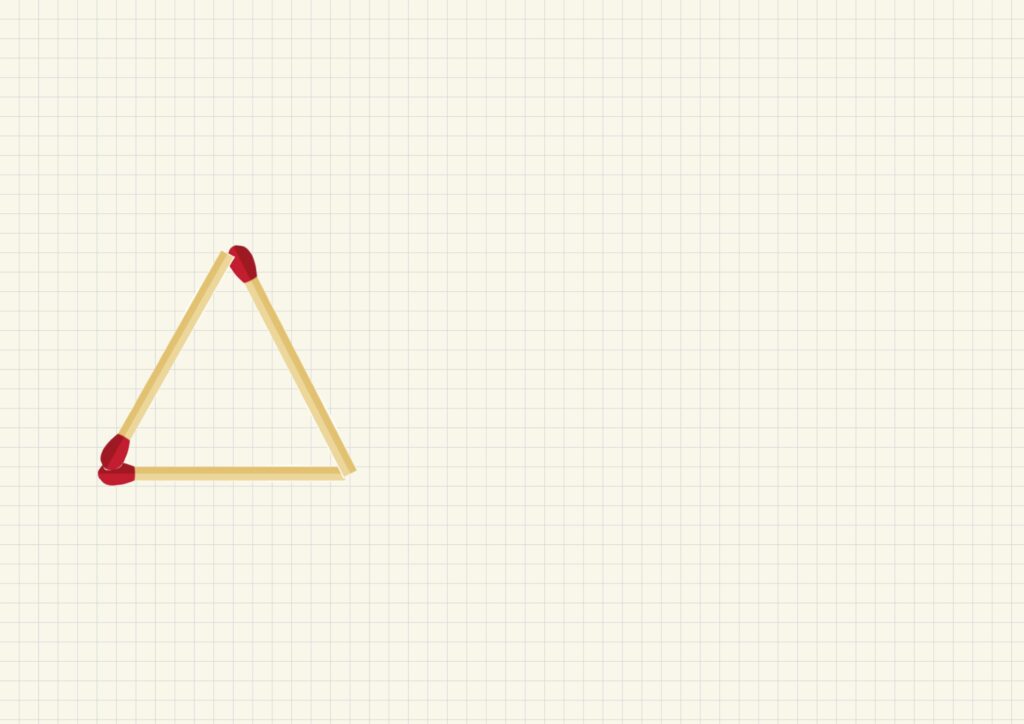
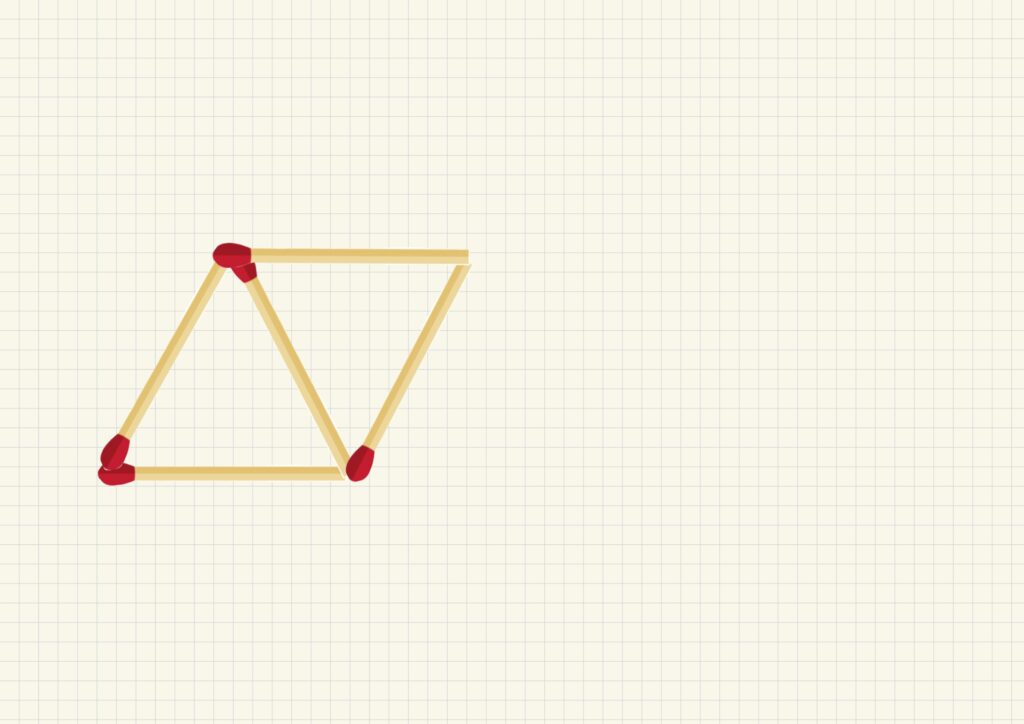
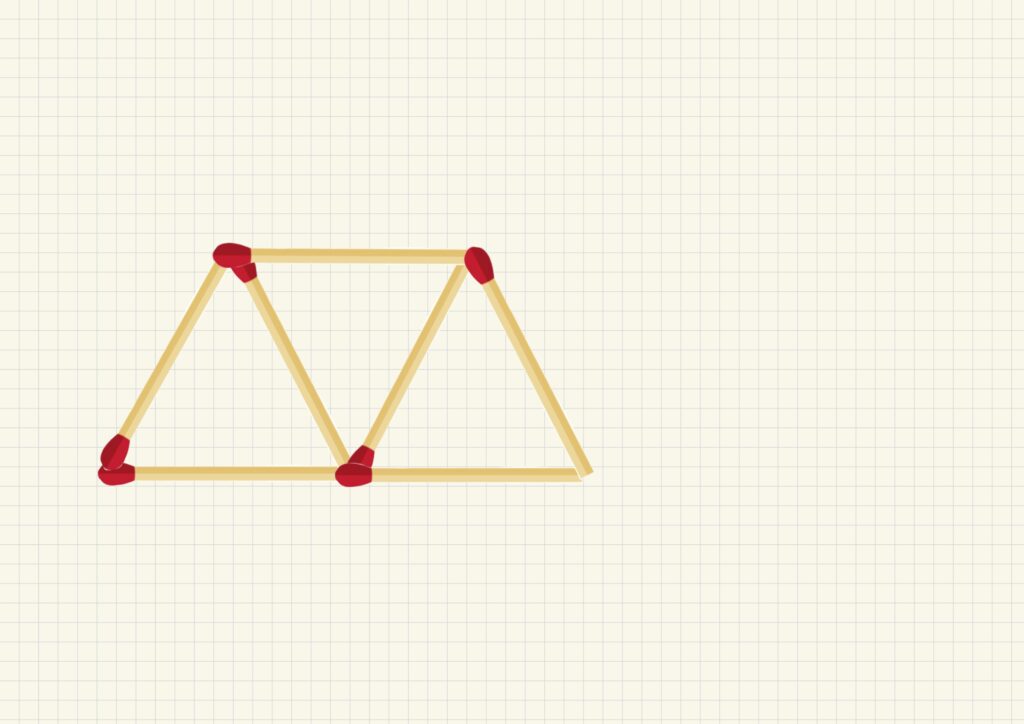
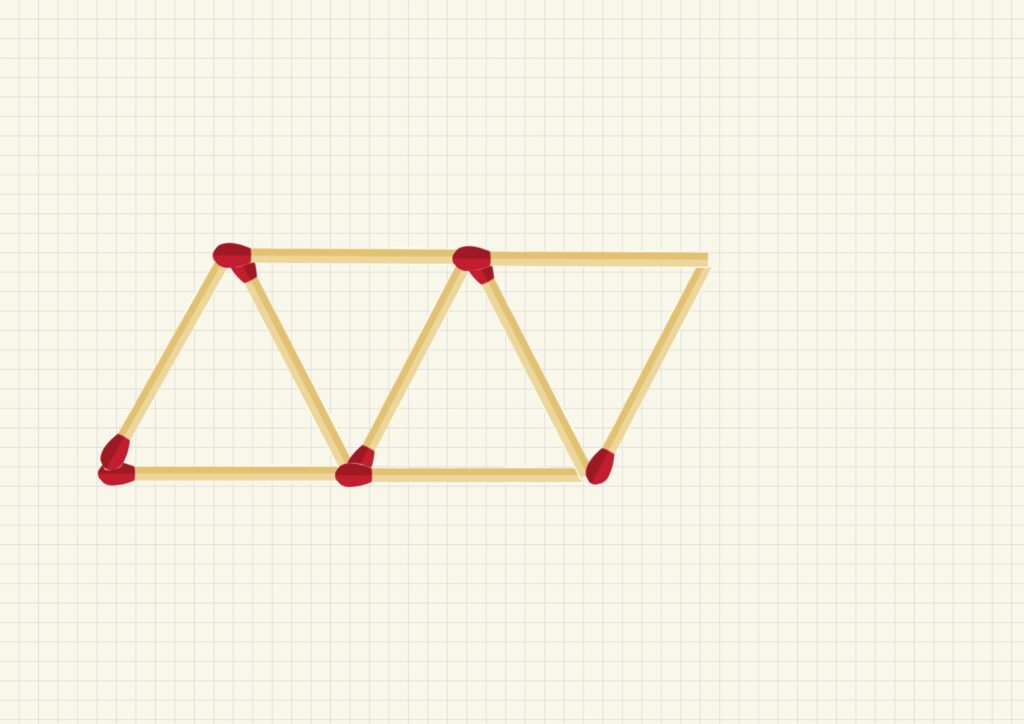
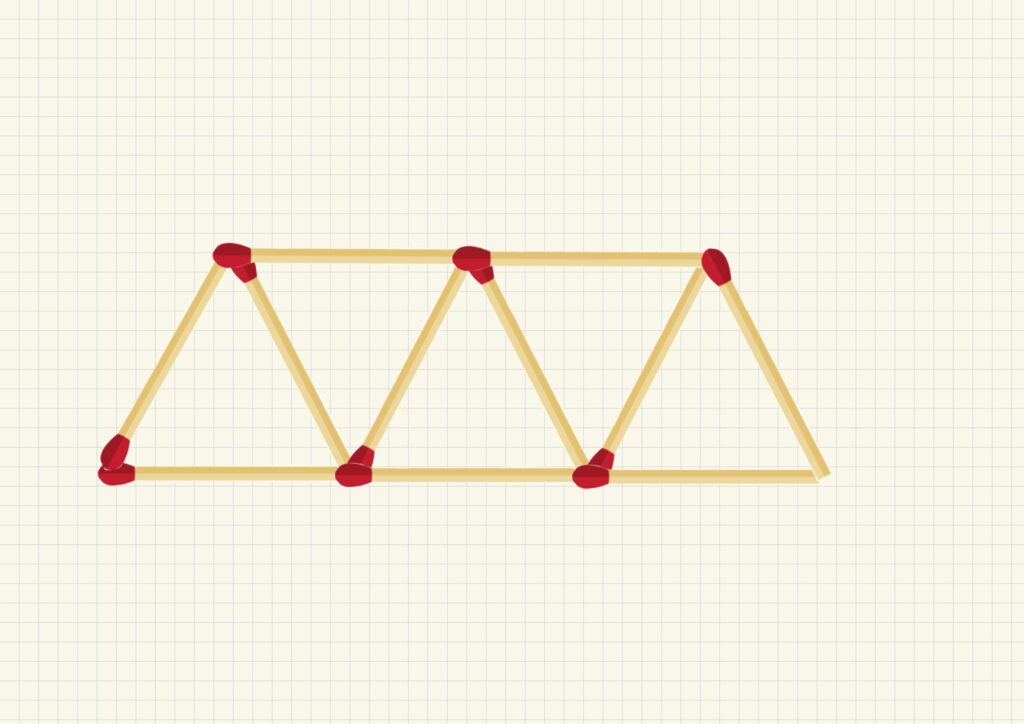
最初の状態（①）で
マッチ棒を３本使用して三角形を作ります。
その後、マッチ棒を２本使って
三角形をどんどん増やしていきます。（②〜⑤）
それぞれの状態（①〜⑤）とマッチ棒の本数
増えた三角形の個数を表にまとめました。
最初の三角形は数えません！
| 状態 | マッチ棒の本数 | 増えた三角形の個数 |
| ① | ３本 | ０個 |
| ② | ５本 | １個 |
| ③ | ７本 | ２個 |
| ④ | ９本 | ３個 |
| ⑤ | 11本 | ４個 |
最初の状態①ではマッチ棒を３本使いました。
その後、最初に作った三角形の横につなげる形で
マッチ棒2本を使って三角形を増やしていきました。
三角形が１つ増えるたびに使用されるマッチ棒は２本ずつ増える
ことが分かります。
増えた三角形の個数とマッチ棒の本数の関係は次のように表せます。
（マッチ棒の本数）＝３＋ 2 ×（増えた三角形の個数）
４個三角形が増えたとし
（増えた三角形の個数）に4を入れてみましょう。
（マッチ棒の本数）＝３＋２×４＝11 11本になります。
上の表でチェックしてみると
増えた三角形の個数が4個のとき
マッチ棒の本数はたしかに11本になっていますね。
お待たせしました。文字の登場です。
（増えた三角形の個数）を文字\(a\)で表します。
すると、マッチ棒の本数は次のように表せます。
（マッチ棒の本数）＝３＋2 × \(a\)
これで、\(a\)に好きな数字を入れるだけで
必要なマッチの本数が分かるようになりました！
もし、三角形を100個作りたいとき
マッチの本数を知る必要がありますね。
最初の三角形を含めて100個なので
増えた三角形の個数は99個です。
先ほどの式の\(a\)に99を入れてみましょう。
（マッチ棒の本数）＝３＋２× 99＝201 となります。
三角形を100個作るためには
201本のマッチ棒が必要であることが分かりました！
このように、文字を使って考えることで
「三角形を100個作りたい！」というような
具体的な状況に応用することができるのです！
少しは文字の便利さを分かってもらえたでしょうか？
少しずつ文字に慣れて、文字の必要性を分かってください！
文字を使う練習
マッチ棒を使って三角形を作るときに
どのように文字を使うかを学びました。
もう少し、文字の使い方に慣れるため
3つの問題に取り組んでみましょう！
問題1
1個120円のドーナツを\(x\)個買います。
（１）代金を文字\(x\)を使って表しなさい。
（２）ドーナツを６個買うとき、代金はいくらになるか？
具体的にドーナツをイメージしてみましょう。
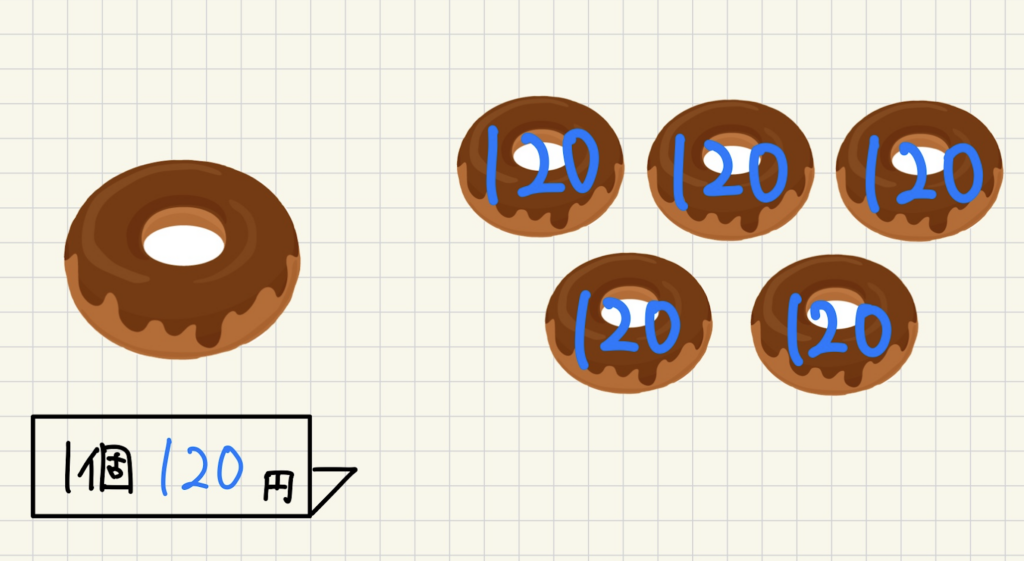
ドーナツを１個買うごとに代金は120円ずつ増加していくことが
イメージできているでしょうか？
ドーナツ１個につき代金が120円増加する
という部分がポイントです。
ドーナツを文字\(x\)でおくと
代金は（代金）＝120 × \(x\)で表せますね。
よって、（１）の答えは120 × \(x\)です。
（２）は簡単ですね。
ドーナツを6個買うということは
\(x\)に６を入れるということです。
120 × ６＝720 答えは720円です。
問題を見たときに、実際にドーナツを書くなど
具体的な状況をイメージすることが大切です。
問題2
１個\(x\)(g)の品物４個を\(y\)(g)の箱に入れたとき
全体の重さを文字\(x\)、\(y\)で表しなさい。
さあ、この状況がイメージできていますか？
実際にこの状況をノートに書いてみましょう！
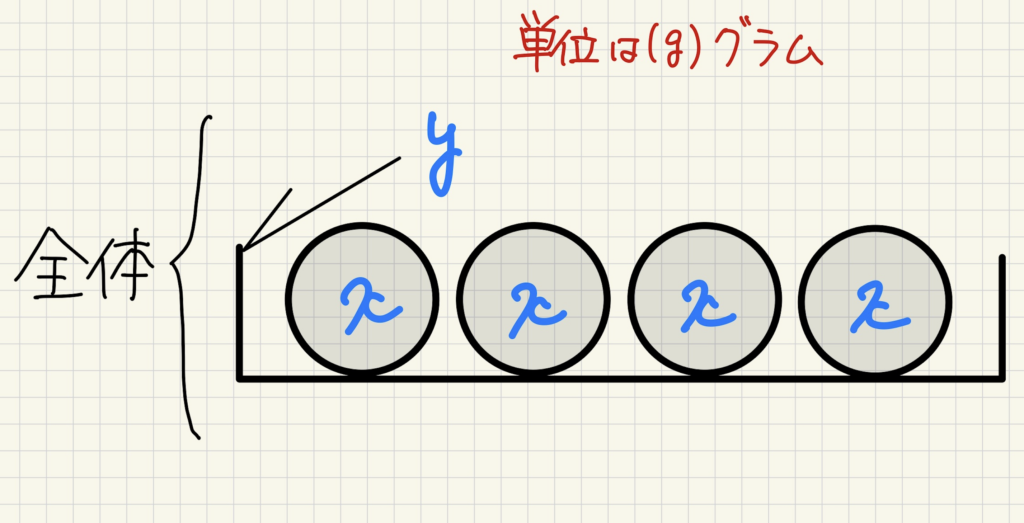
↑１個\(x\)(g)の品物（○）が4つ
\(y\)(g)の箱に入っている様子です。
全体の重さは、（品物４つ＋箱）の重さなので
（全体の重さ）＝４\(x\)＋\(y\) が正解です！
合っていましたか？
【補足】文字を使うときは
文字なのか単位なのかを明確にする必要があります。
この問題のように、グラムやメートルのような単位には
（ ）をつけて区別してあげましょう。
問題3
縦が\(a\)(cm)、横が\(b\)(cm)の長方形がある。
この長方形の面積と周の長さを文字\(a\)と\(b\)で表しなさい。
縦が\(a\)(cm)、横が\(b\)(cm)の長方形がイメージできていますか？
長方形の面積の公式は
（面積）＝（縦の長さ）×（横の長さ）です！
今、縦の長さが\(a\)、横の長さが\(b\)なので
（面積）＝\(a\) × \(b\) が正解です。
周の長さはぐるっと一周長さを足してあげればいいですね。
（周の長さ）＝\(a\)＋\(b\)＋\(a\)＋\(b\)＝2(\(a\)＋\(b\))
分配法則を使って2でまとめてあげたら完璧です！
どうでしたか？
何かを文字で表すときは
状況を理解するために絵や図をかいてみることが大事です！
「分からない！」となったらまず何か書いてみましょう。
コメント