こんにちは!ケントです!
今回は中学数学で学ぶ4種類の作図方法を詳しく解説します!
分かりやすい動画つきです!
このブログを読めば、作図の仕方を完璧にマスターできます!
平面図形の単元で理解度に不安がある場合は以下の記事で復習できます!
作図とは?
作図とは、コンパスと定規を使って図をかくことです!
※図やグラフは「書く」ではなく「かく」が正しい。
作図では、コンパスと定規以外の道具は使えません。分度器は使えません!
また、作図に使った目印の線などは消さずに残しておきましょう!
採点者にどのように作図したのかを伝える必要があるからです。
作図の跡を消すと○をもらえないこともあります!
垂直二等分線とは?
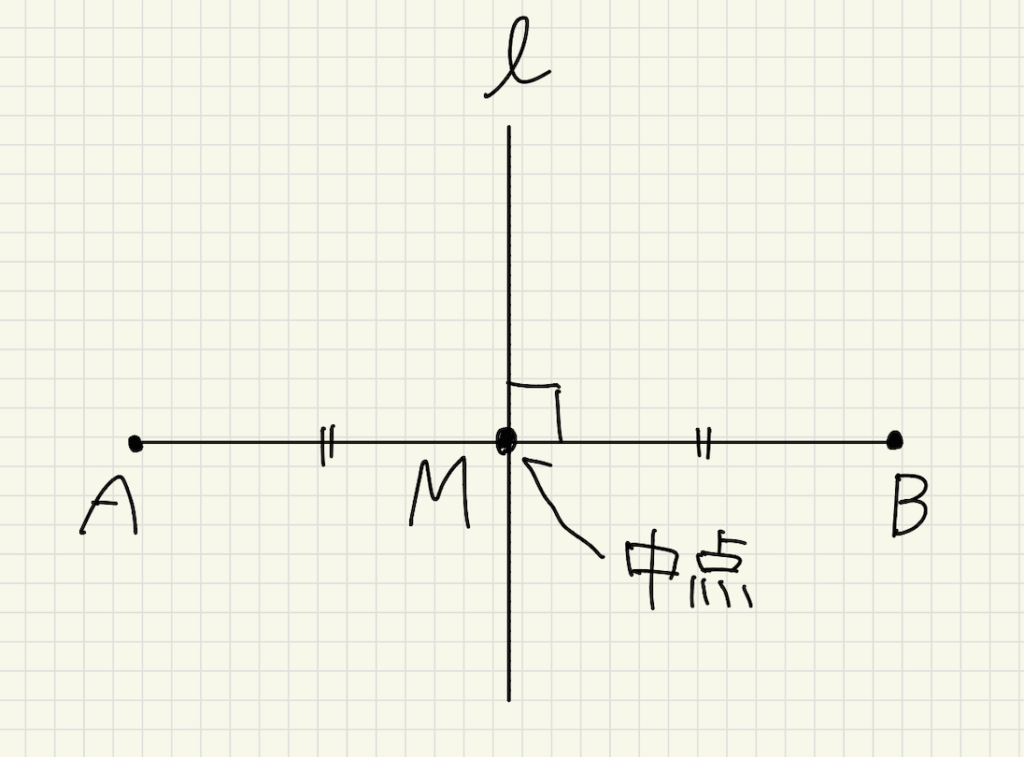
上の図のようにAM=MBのとき、点Mを線分ABの中点と言います。
また、中点Mを通りABに垂直な直線\(l\)を線分ABの垂直二等分線と言います。
ある線分を垂直に二等分する線が垂直二等分線です。
また、垂直二等分線上に点を取るとその点からA,Bまでの距離は等しくなります!
垂直二等分線の作図
初めに垂直二等分線の作図を説明します!
まずは動画で確認してみましょう。こちらの2つがすごく分かりやすいです。
垂直二等分線は次の手順で作図できます!
① 点Aを中心にして適当な半径の円をかく
② 点Bを中心にして①と同じ半径の円をかく
③ ①と②でかいた半円の2つの交点を結ぶ
実際にかけたら
✅ 本当に垂直になっているか?
✅ 線分ABは二等分されているか?
をチェックしてみましょう!
角の二等分線とは?
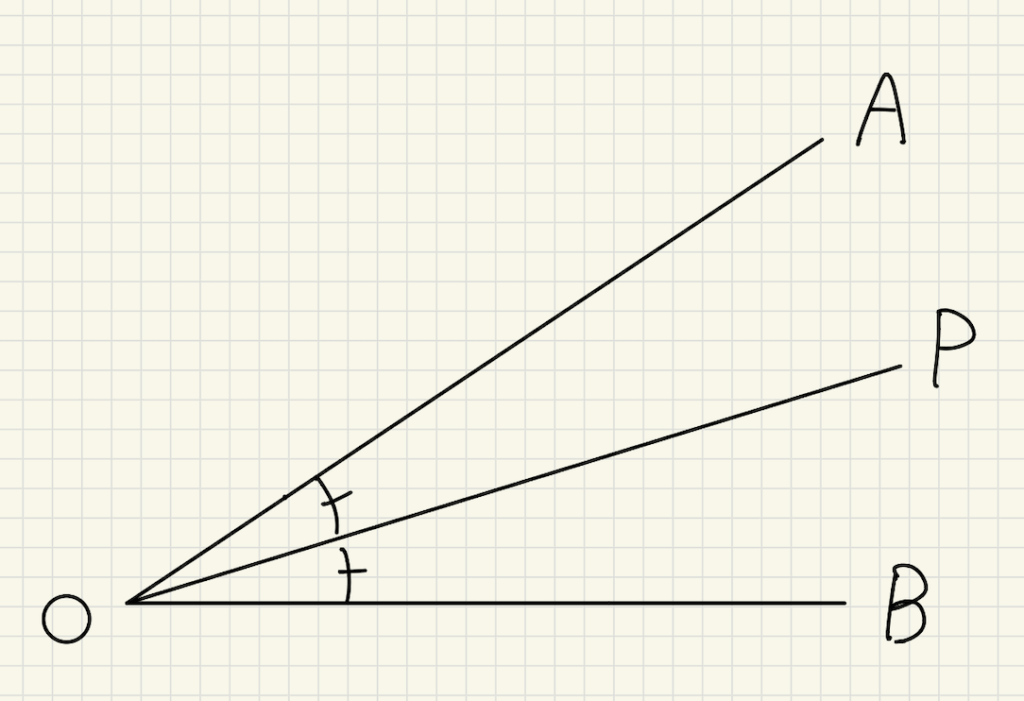
上の図のように、∠AOBを∠AOP=∠BOPに二等分する線分OPを角の二等分線と言います。
角の二等分線上にある点を取ると、半直線OA,OBまでの距離は等しくなります。
角の二等分線の作図
次は、角の二等分線の作図を説明します。
まずは動画で確認してみましょう。こちらの2つがすごく分かりやすいです。
角の二等分線は次の手順で作図できます!
① 点Oを中心とする円をかき、半直線OA,OBとの交点をそれぞれC,Dとする。
② ①でかいたC,Dのそれぞれを中心とする等しい半径の円の交点をPとする。
③ 半直線OPをかく。
実際にかけたら
✅ 本当に二等分されているか
をチェックしましょう。
直線上にある点を通る垂線
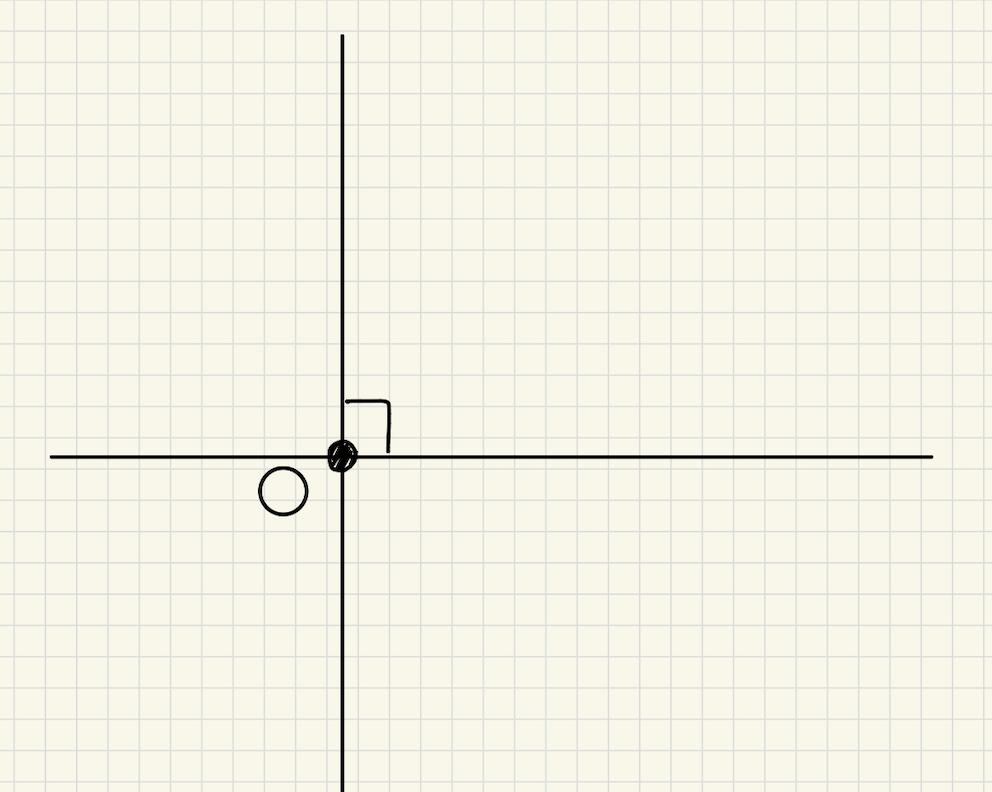
「直線上にある点を通る垂線」とは上の図のように、直線\(l\)上にある点Oを通る垂線のことです。
ほぼ垂直二等分線の作図と同じですがまずは動画で確認しましょう!こちらがとても分かりやすいです。
直線\(l\)上にある点を通る垂線は、次の手順で作図できます!
① 直線\(l\)上の点Oを中心に適当な半径の円をかき、直線\(l\)との2つの交点をそれぞれA,Bとする。
② 点A,Bそれぞれを中心とする等しい半径の円の交点をPとする。
③ 点Oと点Pを結ぶ。
実際にかけたら
✅ 本当に点Oを通っているか?
✅ 本当に垂直になっているか?
をチェックしましょう。
直線上にない点を通る垂線
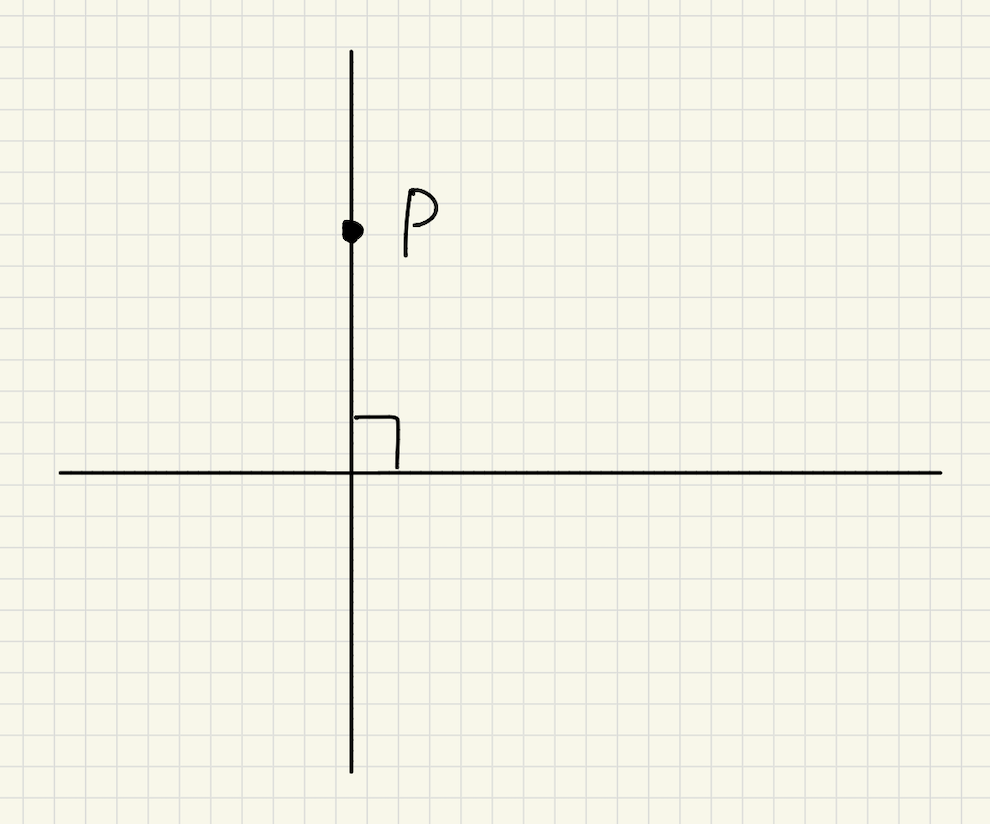
「直線上にない点を通る垂線」とは上の図のように、直線\(l\)上にない点Pを通る垂線のことです。
これの作図方法をまずは動画で確認しましょう!こちらがとても分かりやすいです。
直線\(l\)上にない点を通る垂線は次の手順で作図できます!
① 点Pを中心にして適当な半径の円をかき、直線\(l\)との2つ交点をA,Bとする。
② 点A,Bそれぞれを中心とする等しい半径の円の交点をQとする。
③ 点Pと点Qを結ぶ。
実際にかけたら
✅ 本当に点Pを通っているか?
✅ 本当に垂直になっているか?
をチェックしましょう。
正三角形の作図
最後に、おまけとして正三角形の作図を紹介します!
正三角形はすべての辺の長さが等しい三角形です。
正三角形の作図は定期テストでよく出題されます。
まずは、動画で確認してみましょう。こちらがとても分かりやすいです。
次の手順で正三角形を作図することができます!
① 線分ABをかく。
② 点A,Bそれぞれを中心とする等しい半径の円の交点をPとする。
③ 点PとA,Bそれぞれを結ぶ。
これで正三角形がかけます。とても簡単ですよね!
実際にかけたら
✅ すべての辺の長さが等しいか?
✅ すべての角の大きさが等しいか?
をチェックしましょう。
まとめ
今回は4種類の基本的な作図と正三角形の作図を解説しました!
手順を言葉で暗記するよりも何度もかいてみることで覚えられます。
たくさん作図をしてみましょう!






コメント