平面と直線＆平面と平面 -

平面図形の単元では
点と直線の位置関係（垂直や平行など）を考えました。
（平面図形の復習はコチラから！）

今回は平面と直線の関係、平面と平面の関係について詳しく解説します！

平面って何？

そもそも平面とは
どの方向にも限りなく広がっている平らな面のことです。

みなさんが使っている机の上も平面の一つです。
机は当然限られた面積しかありませんが、
数学ではどの方向にも無限に広がっているものを
平面とみなします。

つまり、平面とは無限に広い机の上の面です。

「地面と平行で、地面から3mの高さの平面」や
「地面に垂直な平面」や
「この壁に対して○°だけ傾いている平面」など

3次元の空間に対して、
平面の作り方はさまざまです。

しかし、ある条件を決めると
これ以外の平面はあり得ない！
というように1つの平面に特定することができます。

その条件を説明します。

平面がただ1つに決まるのは下の4つの場合のみです。

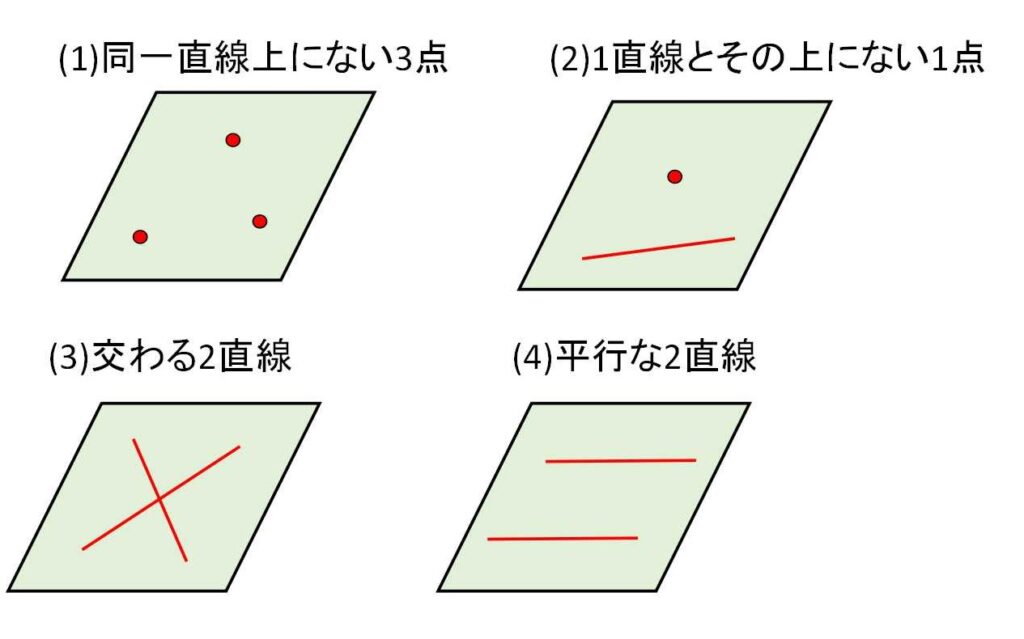
(1)を考えてみましょう。
目の前の空間にてきとうに3点をイメージしてみます。
ここでイメージした3点を通る平面は1つしかないはずです。

では、2点だとどうでしょう？
同じように、目の前の空間に2点をイメージしてみましょう。
2点を通る平面がいくつも存在することに気づきましたか？

3点を含む平面は必ず1つに決まりますが、
1点、2点を含む平面は無数に考えられてしまいます。

写真撮影をするときに三脚を使いますね？
三脚は3点でカメラを支えます。
平面を1つに定めることができるので
グラグラせずに安定するのです！

他の(2)〜(3)についても
本当に言えるかどうか確認してみましょう。

この「平面が1つに決まる条件」は
難しい問題で出されることはありません。
出題されても一問一答でしょう。
暗記してしまうのが早いです。

平面と2直線の関係は下の3パターンのみになります！

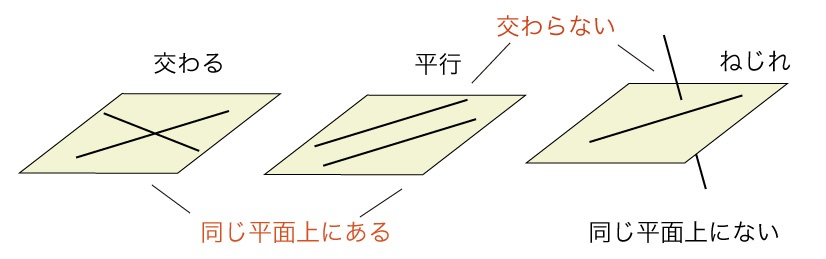
まず同じ平面上で交わる場合、
そして、同じ平面上で平行である場合

以上2つのパターンは
直線が平面上に存在している場合です。

最後は、直線が同じ平面上にないパターンです。
平面と直線が「交わる」わけでも「平行」でもない場合です。

このような位置関係を「ねじれの位置」と言います。

ねじれの位置は少し難しいので立方体で考えてみましょう。

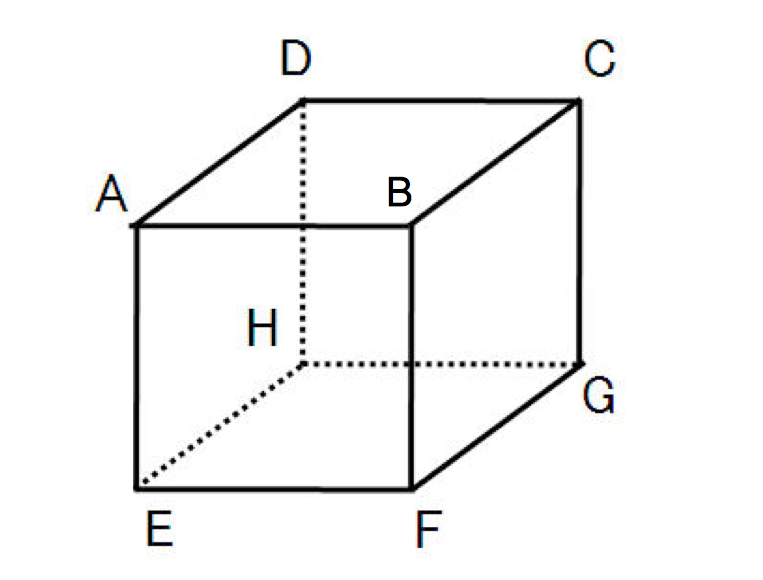
問　辺ABとねじれの位置にある辺をすベて答えなさい。

ねじれの位置にある辺を求める問題を見たら、
「平行な辺」→「交わる辺」の順に探しましょう！

辺ABと平行な辺は
辺DG、辺HG、辺EFの3本です。

辺ABと交わる辺は
辺DA、辺CB、辺EA、辺FBの4本です。

ねじれの位置にある辺は
平行でもなく、交わることもない辺です。

よって答えは、
辺DH、辺CG、辺GF、辺HEの4本となります！

平面と1直線の関係は下の3パターンのみとなります！

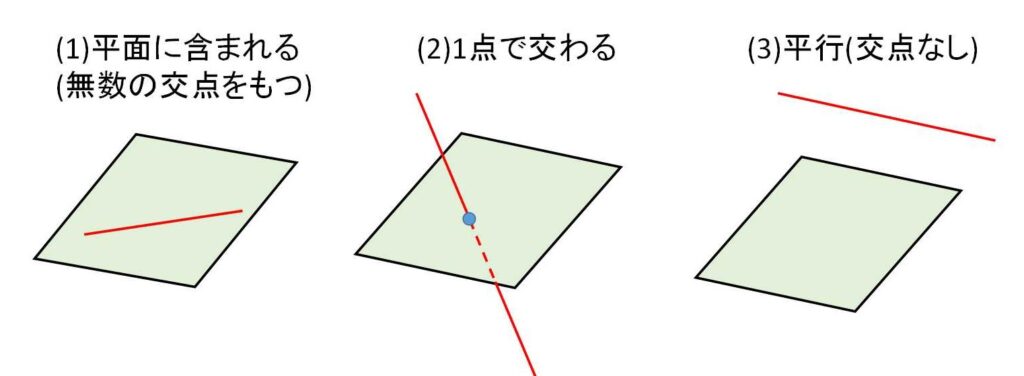
(1)は平面上に直線がある場合です。
直線が平面に含まれると表現します！
「ねじれの位置」のセクションで使用した立方体では
辺ABは一番手前の面に含まれると言います。
この表現は結構重要です。

(2)は平面と直線が1点で交わる場合です。
直線が平面を突き破っているイメージです。

平面に直線が90°の角度で交わっているとき
平面と直線は垂直であると言います。

(3)は平面と直線が交わらず、平行な場合です。

最後は、平面同士の関係を考えます。

平面と平面の関係は下の2パターンのみです！

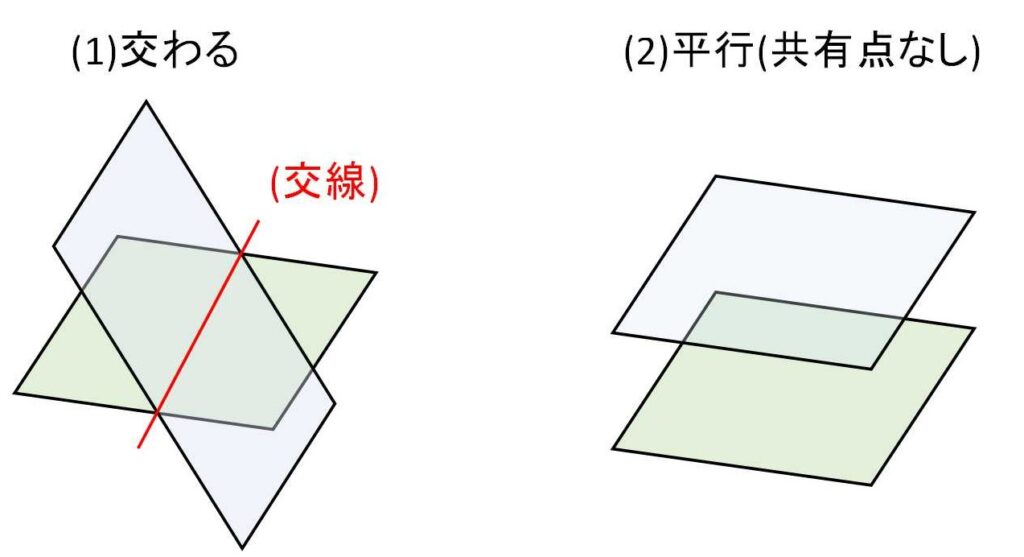
(1)は交わる場合です。
2つの平面の間にできる線を交線と言います。
(2)は平行な場合です。

あまり重要ではないですが、一応知っておきましょう！

平面と直線、平面と平面の関係についてまとめました！

【まとめ】
・平面がただ1つに決まるのは4パターンのみ
・平面と2直線の関係は3パターンのみ
・平行でもなく、交わらない位置関係を「ねじれの位置」という
・平面と1直線の関係は
「交わる」「平行」「含まれる」の3パターンのみ
・平面と平面の関係は2パターンのみ