こんにちは!ケントです!
今回は加法と減法について学んでいきます。
この単元のこれまでの内容は以下のリンクから復習できます!
加法の計算方法
加法は足し算を少しかっこよく言ったものです。中学数学からは、足し算、引き算、掛け算、割り算をそれぞれ加法、減法、乗法、除法と言います。
今回は、次の3種類の計算方法をマスターしましょう!
① +符号の場合 『例:(+2)+(+3)』
② ー符号の場合 『例:(ー2)+(ー3)』
③ 異符号の場合 『例:(+2)+(ー3)』
東西に通じる下の図のような道路を使って考えます。ただし、東(右)を正の向きとします。
<① +符号の場合> (+2)+(+3)
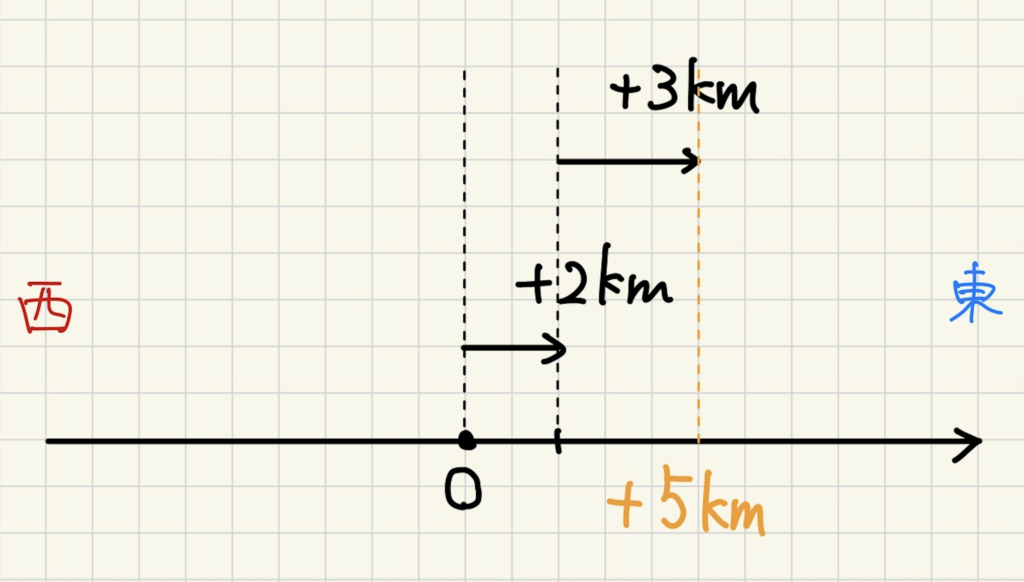
道路の例に直すと原点から東に2進み、そこからさらに東に3進むと表現できます。この場合、原点から5kmだけ東にいることになります。
+符号同士の加法は小学校で学んだ足し算とまったく同じです。シンプルに2+3=5で5と答えてあげればOKです。
<② ー符号の場合> (ー2)+(ー3)
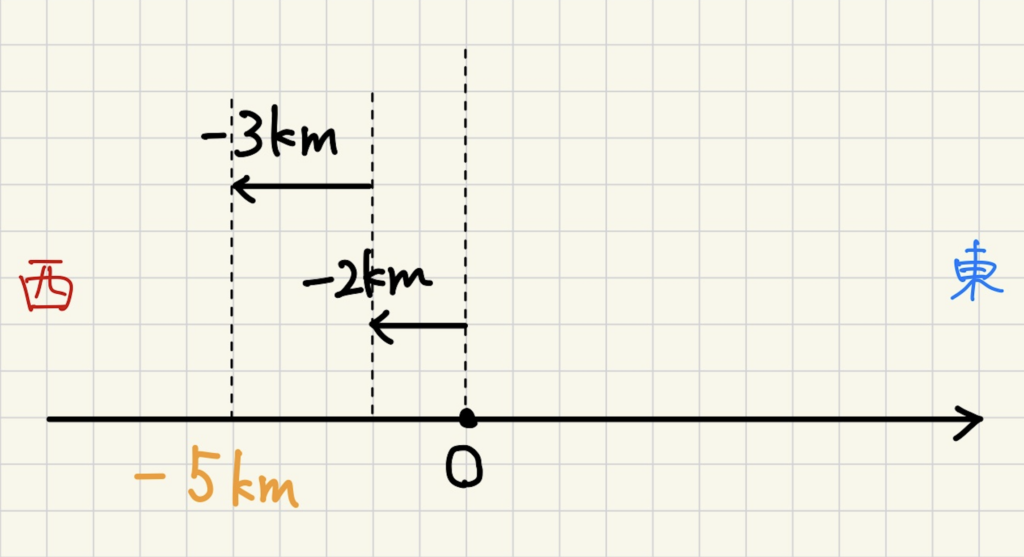
今は、東に進むことを正としているのでー(マイナス)の数は反対向きの西に進むことを意味します。
すなわち、原点から西に2進み、さらにそこから西に3進むと表現できます。この場合、原点から西に5kmだけ西にいることになります。
つまり、ー符号同士の加法は「絶対値同士を足して、符号をつけてあげる」ことで計算できます。
具体的に、(ー4)+(ー5)の計算をします。
まず、絶対値4と5を足して9。ー4もー5も符号はーなので、絶対値9にーをつけてあげて答えはー9となります。
<③ 異符号の場合> (+2)+(ー3)
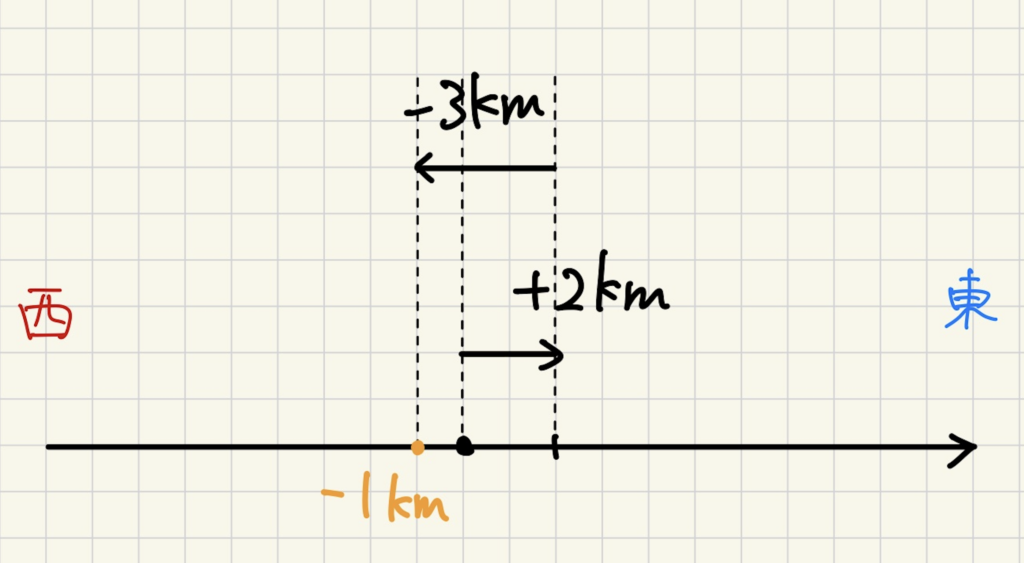
正の数と負の数同士の足し算です。
同じように道路上で考えると、原点から東に2進み、そこから西に3進むと表現できます。
するとどうでしょう?今いる位置は、原点から西に1進んだ場所になります。
(+2)+(ー3)の答えはー1になりました。
異符号同士の足し算は「逆向きに進む」という考え方で計算することができます。
②と③の場合について、足し算なのに答えがマイナスになるのは気持ち悪いかもしれませんが
左向き(負の向き)に進む数を考えているため不思議なことではありません。
以上が、中学数学でやる加法の計算の仕方です!
それでは、加法の演習問題をやってみましょう。
次の①〜③の計算をしなさい。
①(+1)+(+3)
②(ー4)+(ー2)
③(ー1)+(+3)
減法の計算方法
減法は引き算を少しかっこよく言ったものです。
加法と同じように、2種類の計算方法をマスターしましょう!
① 正の数を引く場合 『例:(+2)ー(+3)』
② 負の数を引く場合 『例:(+2)ー(ー3)』
<① 正の数を引く場合>(+2)ー(+3)
ある数から正の数を引く計算は小学校まででやってきた引き算とまったく同じやり方です。
(+2)-(+3)は2-3と直して計算して、答えは-1となります。
<② 負の数を引く場合>(+2)ー(ー3)
ある数から負の数を引く場合は注意が必要です。
正の数と負の数でやったことを思い出してください!
「2個増える」ことは「-2個減る」ことと同じ意味でしたね。また「階段を7段上がる」ことは「階段を−7段下がる」ことと同じでした。
(+2)ー(ー3)も同じように考えると「2から-3を引く」ことは「2から(に)3を足す」ことと同じです!
(+2)-(-3)=(+2)+3=5が答えになります。
負の数を引くときは次のことに注意してください!(超超大切!)
ー(ーA)は+Aに直して計算する!
具体的に、ー(ー6)=+6です。
以下のような、負の数を引く計算が出てきた時は、絶対に符号を+に変えて計算しましょう!
【負の数を引く計算の例】
①5ー(ー4) → 5+4
②ー3ー(ー2)→ ー3+2
以上が、中学数学でやる減法の計算の仕方です!
それではここで、減法の演習問題をやってみましょう。
次の①〜③の計算をしなさい。
①(ー2)ー(+3)
②(+4)ー(ー2)
③5ー(ー3)
まとめ
【加法】
・正の向きと負の向きを考えると良い!
【減法】
・負の数同士の計算は絶対値に-をつける
・-(-A)=A






コメント