ヒストグラムとは？ -

「データの分析」の最初の内容です。
今回は、範囲、ヒストグラム、度数分布表について
詳しく解説します！

データの分析とは？

そもそもデータの分析とは
与えられた数値などの情報から
その傾向や特徴を見出すことです。

小学校の算数では、平均値や中央値などの代表値を使って
データの分析を行いました。

中学校の数学では、ヒストグラムや箱ひげ図と呼ばれる
ものを利用してデータの分析を行います！

データの分析を行う1つの指標に
「範囲（レンジ）」というものがあります。

範囲＝最大値－最小値

で求められます！

具体的に次のような
中学生のソフトボールの記録があります。

【記録】11　12　13　15　15　16　17　21　22　24
　　　　24　25　26　26　27　28　30　33　37　38　(m)

このとき、最小値は11(m)であり、最大値は38(m)です。
よって、このデータの範囲は
38－11＝27　27(m)となります！

範囲はこれだけの計算ですが
計算式を覚えていない子が多いです！要チェック！

あるクラスの生徒の家から学校までの通学時間は
次の通りです。

【記録】5　5　5　11　11　11　12　12　16　17　17　17
　　　18　18　19　19　21　21　21　21　25　25　26　30　(分)

これをもとに度数分布表を作成すると下の図のようになります。

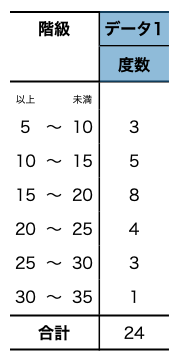
これを柱状グラフにすると下の図のようになります。

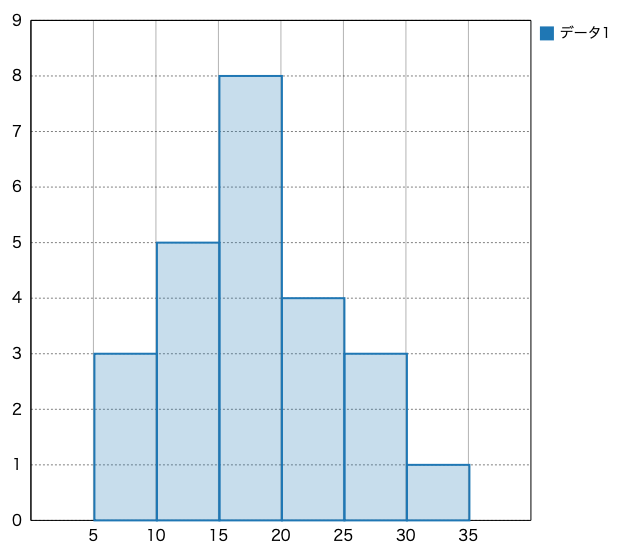
このようにデータを柱状グラフにしてまとめたものを
ヒストグラムと言います！

このデータでは5分以上10分未満、10分以上15分未満、
15分以上20分未満…のように
5分ごとに区切っています。

5分以上10分未満、10分以上15分未満…のことを階級と言い、
区切られた区間の幅を階級の幅と言います。
今回は階級の幅は5(分)です！

度数分布多角形は下の図のように
ヒストグラムの長方形の上の辺の中点を
結んでできる多角形のことです。

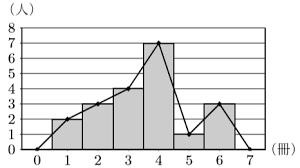
または、度数折れ線と言う場合もあります。

ヒストグラムについてまとめました！

【まとめ】
・範囲＝最大値－最小値
・柱状グラフをヒストグラムと言う
・区間の幅を階級の幅と言う
・柱状グラフの長方形の上の辺の中点を結んだ
グラフを度数分布多角形または度数折れ線と言う