今回は表面積と体積について具体例を使って
詳しく解説します！
また、実際に表面積や体積を求めてみます！
「空間の図形」については
以下のリンクから復習できます！
いろいろな立体
✅ 角柱、円錐、正多面体って何？
平面と直線＆平面と平面
✅ ねじれの位置や「面に含まれる」の意味が分からない！
動かしてできる立体
✅ 回転体とか母線って何？
投影図と展開図
✅ 投影図、立面図、平面図って何？
表面積とは？
「表面積」と言われてもどこを指しているのか
いまいち分からないという子が多いです。
ここで、しっかりと覚えましょう！
表面積とは底面積と側面積を合わせた面積です。
簡単に立体の外側のすベての面のことです。
立体を手に取ってさまざまな角度から眺めたとき
自分の目で見ることができる部分すべてが表面積です。
具体的に、下の直方体を見てみましょう。
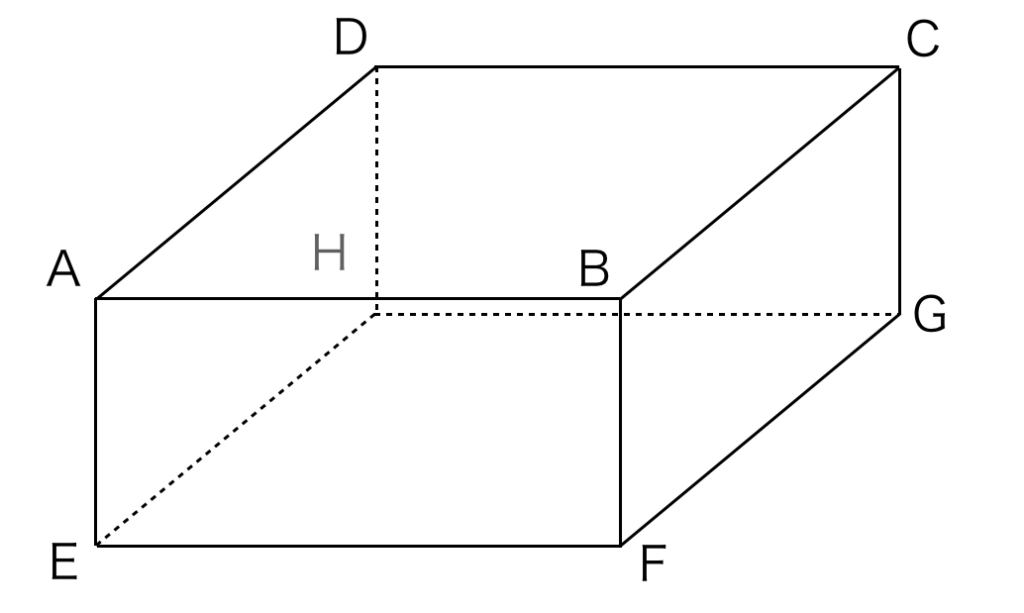
一番手前の面ABFE、それと対面にある面DCGH
底面と言える面ABCD、それと対面にある面EFGH
横の面の面ADHE、それと対面にある面BCGF
この6つの面をすべて合わせたものが表面積です！
角柱、角錐の表面積の求め方
表面積を求めるときは展開図をかいてみると良いです！
例えば、正三角柱の展開図は下のようになります。
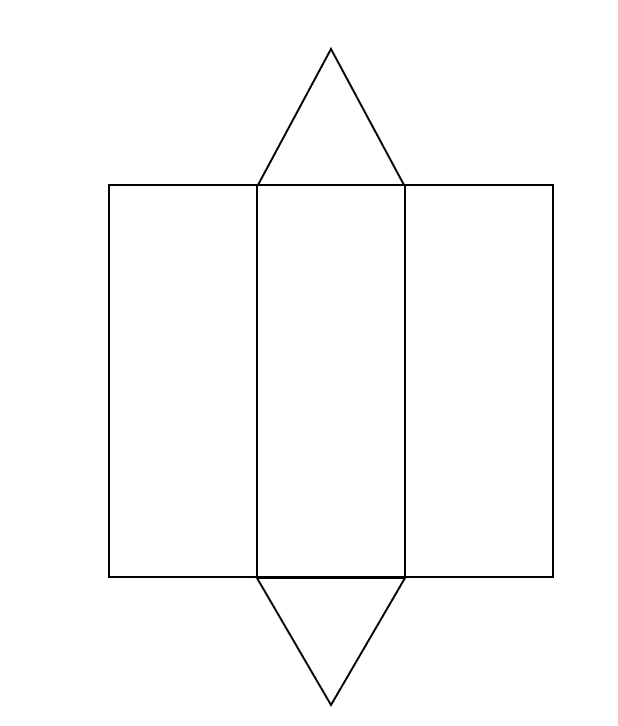
正三角形の面積を4cm2、長方形1つの面積を36cm2とすると
表面積＝底面積＋側面積
＝（正三角形）×2＋（長方形）×3
＝4×2＋36×3＝116(cm2)となります！
また、正四角錐の展開図は下のようになります。
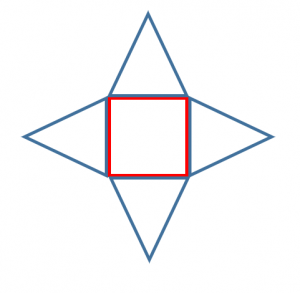
真ん中の正方形の一辺が6cm、4つの三角形の高さも6cmとする。
表面積＝底面積＋側面積
＝真ん中の正方形＋(三角形の面積)×４
＝6×6＋(6×6÷2)×4
＝108(cm2) となります！
円柱、円錐の表面積の求め方
まず、円柱の展開図は下のようになります！
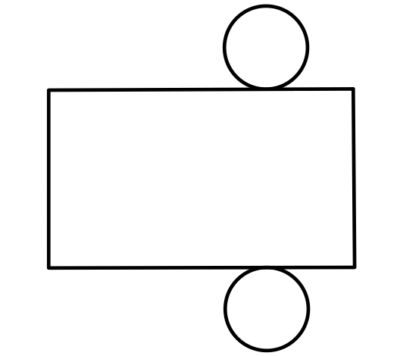
円の半径を4cm、長方形の縦方の辺の長さを8cmとする。
また、長方形の横の長さは円の円周に等しいので
8πcmとなります。
表面積＝底面積＋側面積
＝(円)×2＋長方形の面積
＝16π×2＋8π×8＝96π(cm2)となります！
円柱の展開図で、長方形の横の長さは円周に等しい！
円柱や円錐などの曲面をもつ立体は
面積や体積にπが含まれることに注意してください！
円錐の展開図は下のようになります。
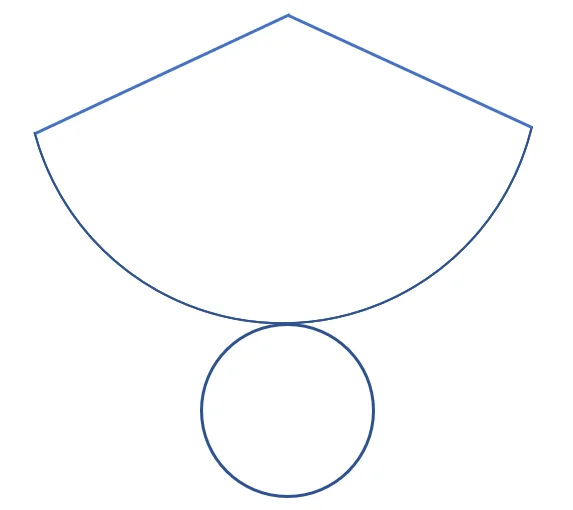
円の半径を3cm、扇形の半径を9cmとする。
扇形の孤の長さは円の周の長さに等しいので
すなわち、扇形の孤の長さは6πcmです。
扇形は円の一部で、18πcmのうちの6πcmは
6÷18＝1/3なので
図の扇形の面積は半径9cmの円の1/3の大きさです！
以上より、
表面積＝底面積＋側面積
＝円＋扇形
＝3×3×π＋9×9×π×(1/3)
＝36π(cm2) となります！
扇形の孤の長さは円の円周に等しい！
円錐の表面積を求める問題は非常によく出題されます！
絶対にできるようにしましょう！
角柱、円柱の体積の求め方
【角柱と円柱の体積の公式】
体積＝底面積×高さ
かっこよく文字を使って表すと
\(V=Sh\)となります！（\(V\)は体積、\(S\)は底面積、\(h\)は高さ）
角錐、円錐の体積の求め方
角錐と円錐は先が尖っている立体です。
同じ底面積、同じ高さの角柱と円柱よりも
体積は小さくなります！
どれくらい小さくなるかというと
角柱や円柱の3分の1になります！
【角錐、円錐の体積の公式】
体積＝底面積×高さ×\(\frac{1}{3}\)
かっこよく文字を使って表すと
\(V=\frac{1}{3}Sh\)となります！（\(V\)は体積、\(S\)は底面積、\(h\)は高さ）
球の表面積と体積
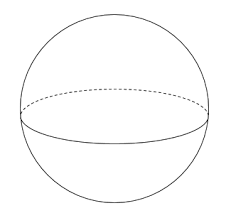
球の体積と表面積は絶対に公式を覚えましょう！
【球の表面積の公式】
（表面積）＝4×π×半径2
「表面(表面積)に心配(4π)あるある(r×r)」のような語呂合わせで覚えました！
かっこよく文字を使って表すと
\(S=4πr^2\)となります！（\(S\)は表面積、\(r\)は半径）
【球の体積の公式】
（体積）＝\(\frac{4}{3}\)×π×半径3
「身(3)の上に心(4)配(π)ある、参上(r3)」のような語呂合わせで覚えました！
かっこよく文字を使って表すと
\(V=\frac{4}{3}πr^3\)となります！（\(V\)は体積、\(r\)は半径）
まとめ
表面積や体積の求め方についてまとめました！
・表面積は底面積と側面積を合わせた部分
・展開図をかくと、表面積を求めやすい！
・扇形の孤の長さは円周に等しい
・角柱、円柱の体積は\(V=Sh\)
・角錐、円錐の体積は\(V=\frac{1}{3}Sh\)
・円の表面積は\(S=4πr^2\)
・円の体積は\(V=\frac{4}{3}πr^3\)
コメント