比例の式の求め方

こんにちは！ケントです！

今回は、与えられた問題文やグラフから比例の式を求める方法を解説します！

オリジナル問題はこの記事の最後にあります！

比例について以下の記事でこれまでの復習ができます！

比例の式を求めるとは？

比例の式を求めるとは、与えられた情報をもとに\(y=ax\)の式を決めることです。

\(y\)と\(x\)は変数なので比例定数\(a\)を求めることと言い換えることができます！

問題①

\(y\)が\(x\)に比例し、\(x=3\)のとき\(y=12\)である。このとき\(y\)を\(x\)の式で表しなさい。

まず、「\(y\)が\(x\)に比例する」と書かれている時点で、求める式の形は\(y=ax\)になります。

答えは\(y=ax\)の形になるということです。

\(x=3\)のとき、\(y=12\)なので、（3,12）の座標を代入すると

\(12=a\times 3\)となり
\(a=4\)となります。

あとは\(y=ax\)に\(a=4\)を代入して
答えは\(y=4x\)です。

重要

「\(y\)が\(x\)に比例する」→「\(y=ax\)」とおく！

問題②

\(y\)が\(x\)に比例し、\(x=2\)のとき\(y=-8\)である。このとき\(y\)を\(x\)の式で表しなさい。

先ほどと同じように「\(y\)が\(x\)に比例する」と書かれているので、まず、\(y=ax\)とおきます。

そして、\(x=2\)のとき\(y=-8\)なので、（2,-8）の座標を代入すると

\(-8=a\times 2\)となり
\(a=-4\)となります。

答えは\(y=-4x\)です！

比例定数が負の場合も同じように計算すればOKです！

次は、グラフから比例の式を求める問題をやってみましょう！

問題③

次のグラフの式を\(y\)と\(x\)で表しなさい。

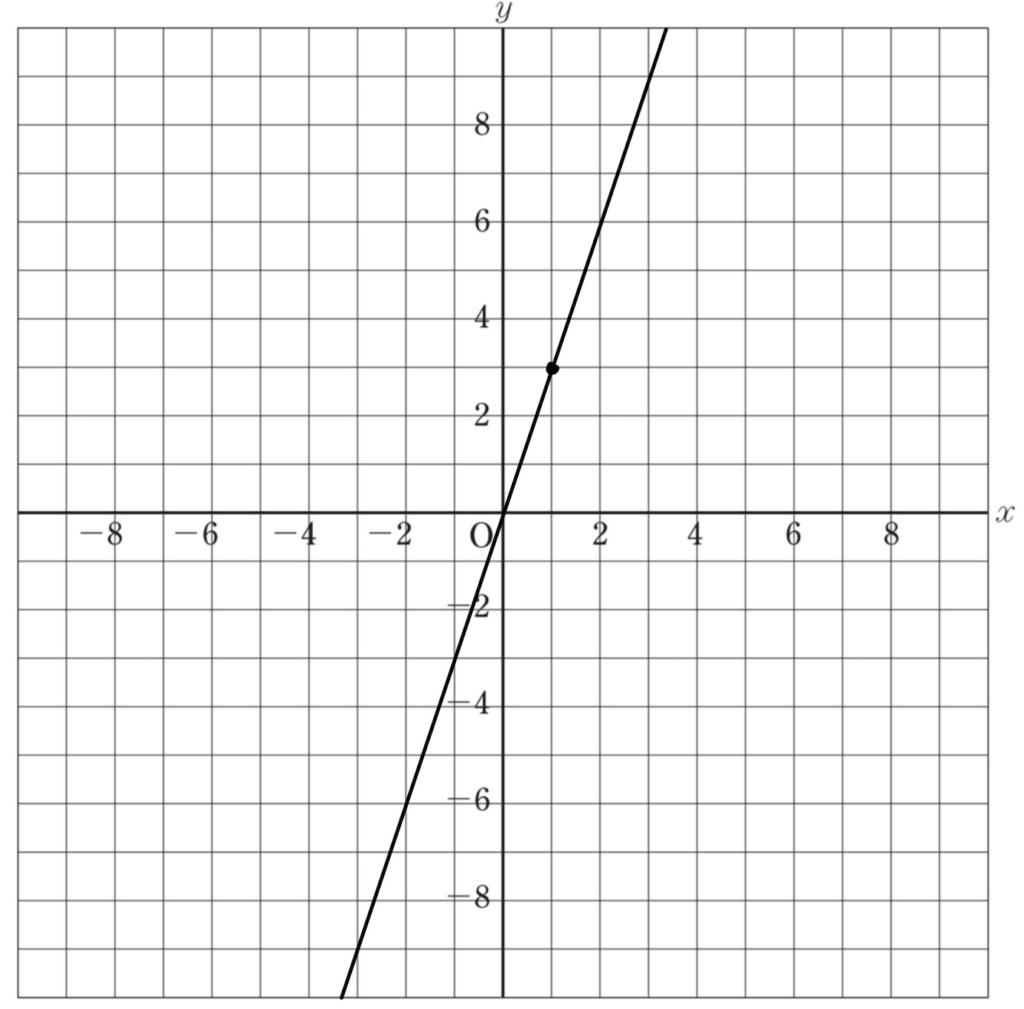
このグラフは直線で原点を通るので比例のグラフです。

比例のグラフと分かった時点で、求める答えは\(y=ax\)という形になります。

あとはこの直線が通る具体的な座標を見つけます。

（1,3）を代入すると、\(3=a\times1\)となります。

\(a=3\)となり、答えは\(y=3x\)です。

代入する座標は（1,3）以外でもOKです！

（-1,-3）や（-3,-9）でも、直線が通っている部分ならどこを代入しても構いません！

比例の式を求める問題についてのまとめを書きました！

【まとめ】
・「\(y\)が\(x\)に比例する」＝\(y=ax\)
・グラフの問題　→　直線が通る点を\(y=ax\)に代入する

基本的な問題を含むオリジナルプリントを作成しました！ぜひ活用してください！