反比例の式の求め方

こんにちは！ケントです！

今回は反比例の式である\(y=\frac{a}{x}\)の求め方について分かりやすく解説します！

オリジナル問題はこの記事の最後にあります！

また、これまでの比例・反比例の内容は以下の記事で復習することができます。

反比例の式を求めるとは？

「反比例の式を求める」とは\(y=\frac{a}{x}\)を決定することです。

\(x\)と\(y\)は変数なので比例定数\(a\)を求めることと言い換えられます。

問題①

\(y\)が\(x\)に反比例し、\(x=2\)のとき\(y=8\)である。このとき\(y\)を\(x\)の式で表しなさい。

まず、「\(y\)が\(x\)に反比例する」と書いてある時点で、求める式は\(y=\frac{a}{x}\)になることが分かります。

答えの形が\(y=\frac{a}{x}\)になるということです。

次に、「\(x=2\)のとき\(y=8\)」と書いてあるので(2,8)をこの式に代入します。

\(8=\frac{a}{2}\)となり、これを計算すると\(a=16\)となります。

最後に、\(a=16\)を\(y=\frac{a}{x}\)に代入して、答えは\(y=\frac{16}{x}\)となります。

「\(y\)は\(x\)に反比例する」→「\(y=\frac{a}{x}\)」

問題②

\(y\)は\(x\)に反比例し、\(x=3\)のとき\(y=-9\)である。このとき\(y\)を\(x\)の式で表しなさい。

まず、まず、「\(y\)が\(x\)に反比例する」と書いてある時点で、求める式は\(y=\frac{a}{x}\)になります。

次に、「\(x=3\)のとき\(y=-9\)」と書いてあるので(3,-9)をこの式に代入します。

\(-9=\frac{a}{3}\)となり、これを計算すると\(a=-27\)となります。

答えは\(y=\frac{-27}{x}\)となります。

比例定数が負の場合も式を求める方法は同じです！

次は、グラフから式を求める問題をやってみましょう！

問題③

次のグラフで表される関数の式を\(y\)と\(x\)で表しなさい。

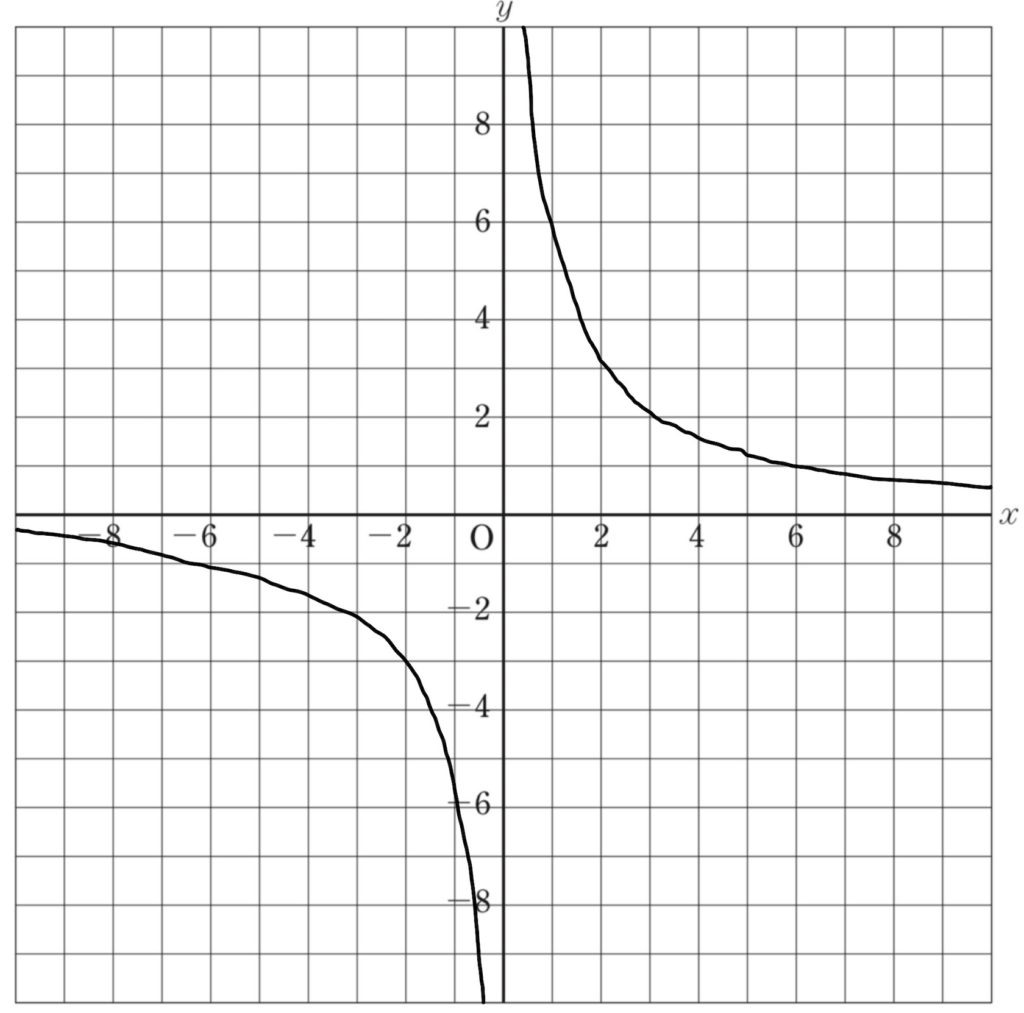
グラフの問題では、1つの座標を\(y=\frac{a}{x}\)に代入する！

このグラフは(1,6)を通っているので、\(y=\frac{a}{x}\)に(1,6)を代入します。

\(6=\frac{a}{1}\)となり、これを計算すると\(a=6\)となります。

よって、答えは\(y=\frac{6}{x}\)となります！

【注意】代入する座標はどこでもいい

(2,3)でも(-6,-1)でも、通っている座標ならどこを代入してもOKです！答えは同じになります。

反比例の式を求める問題についてのまとめを書きました。

【まとめ】
「\(y\)は\(x\)に反比例する」→「\(y=\frac{a}{x}\)とおく」
グラフの問題では、通っている座標を代入する

基本問題を集めたオリジナル問題を作りました！

反比例の式を求める問題が完璧にできるようにぜひ活用してください！