こんにちは!ケントです!
今回は代表値(最頻値、平均値、中央値)について分かりやすく解説します!
「データの分析」について以下のリンクから復習できます!
代表値
データの分析における代表値とはデータの特徴や傾向を表す指標のことです!
主な代表値は最頻値、平均値、中央値です。
最頻値:度数の一番大きい階級の階級値
平均値:データの平均
中央値:データの真ん中の値
それぞれの代表値について詳しく解説します!
最頻値
最頻値は「最」も「頻」繁に現れる値のことです。
度数が最も大きな階級の階級値が最頻値です。
下の度数分布表はある中学校の通学時間を整理したものです。
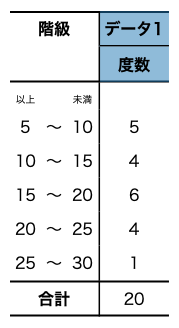
この度数分布表で最も度数の大きい階級は「15以上20未満」ですね。
答えは「15以上20未満」の階級値17.5です!
⚠️階級値は階級の真ん中の値を答えます。ここでは15と20の真ん中である17.5
平均値
「平均」は聞いたことがあると思います。
あるテストで5人の点数がそれぞれ60点、70点、80点、90点、100点の場合
平均点は(60+70+80+90+100)÷ 5=80
平均点は80点になりますね!
度数分布表についても同じように平均値を求めます。
テストの点数のように〇〇分という値ではなく、5以上10未満のように階級で与えられる場合は階級値を使います!
階級値は上から7.5、12.5、17.5、22.5、27.5です。
また、それぞれの度数が上から5、4、6、4、1なので
(7.5×5+12.5×4+17.5×6+22.5×4+27.5×1)÷ 20
=310÷20=15.5
答えは15.5(分)です!
少し計算がややこしいですが、テストの点数の平均点を出すやり方と同じです!
中央値
中央値は「中央」とついているように上から数えても下から数えてもちょうど真ん中にある値のことを指します。
例えば、ソフトボール投げの記録が
【記録】11 12 13 15 15 16 19 20 21 24 25 (m)
となった場合、前から数えても後ろから数えてもちょうど真ん中にある値は16(m)です!
よって中央値は16となります。
記録が偶数の場合はどうするの??
いい質問です!
5や9のようにデータの個数が奇数の場合はちょうど真ん中の値が存在します。
(5の場合) ○ ○ ● ○ ○
(9の場合) ○ ○ ○ ○ ● ○ ○ ○ ○
しかし、4や8のような偶数の場合はちょうど真ん中の値が存在しません!
その場合は真ん中に最も近い2つの値の平均をとります!
これはとても重要です!
【4の場合】
1 2(真ん中)3 4
真ん中に近いのは2と3でこれの平均は
(2+3)÷ 2=2.5
【8の場合】
1 2 3 4(真ん中)5 6 7 8
真ん中に近いのは4と5でこれの平均は
(4+5)÷ 2=4.5
データが奇数個の中央値は真ん中に近い値の平均をとる
度数分布表を使う場合について考えます。

中央値はちょうど真ん中の値です。合計は20なのでデータの個数は偶数個です。
10番目と11番目のデータの平均が中央値なので中央値が含まれているのは「15以上20未満」の階級ですね。
まとめ
代表値についてまとめました!
・最頻値は最も度数の大きい階級の階級値
・平均値は階級値×度数の合計の平均
・中央値はちょうど真ん中の値
→データの個数が偶数のときは真ん中に近い2つの値の平均をとる





コメント