こんにちは!ケントです!
今回は図形の3つの移動について解説します!
以下の記事でこれまでの復習ができます
3種類の移動
まず、図形の移動とはその大きさや形を変えずに他の位置に動かすことです。
図形の移動には次の3種類があります。
平行移動
回転移動
対称移動
それぞれの移動について詳しく解説します。
平行移動
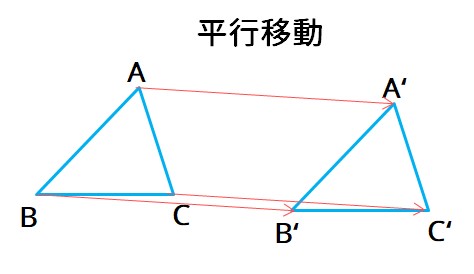
上の図のように図形をある方向に一定の長さだけずらす移動を平行移動と言います。
もとの図形と平行移動させた図形では、次のような特徴があります。
・もとの図形と平行移動させた図形は対応する辺はどれも平行
・対応する点を結ぶ線分は平行で長さが等しい
※対応する点、線分とはAとA’、ABとA’B’のように移動の前後で同じ部分に当たる点や線分のことです。
回転移動
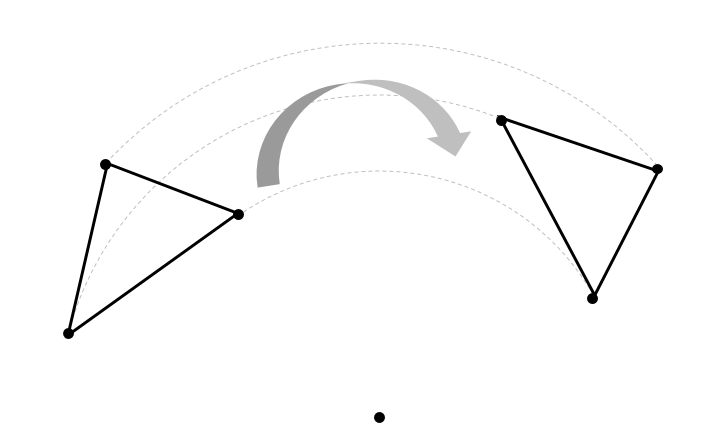
上の図のように図形をある点を中心にとして一定の角度だけ回す移動を回転移動と言います。
また、点Oを回転の中心と言います。
さらに、下の図のように180°回転させる回転移動を点対称移動と言います。
点対称移動は回転移動の仲間です!
もとの図形と回転移動させた図形では次のような特徴があります。
・回転の中心は対応する2点から等しい距離にある
・回転の中心と対応する点を結んでできる角
(∠AOA’や∠BOB’のこと)はすべて等しい
対称移動
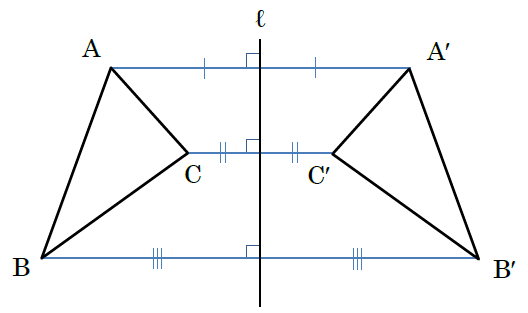
上の図のように図形をある直線\(l\)を軸にして裏返す移動を対称移動と言います。
また、直線\(l\)を対称の軸と言います。
⚠️「対称」の字に気をつけてください!「対象」「対照」ではありません。
もとの図形と対称移動させた図形では、次のような特徴があります。
対称の軸は対応する点を結ぶ線分を垂直に二等分する
まとめ
ここまで平行移動、回転移動、対称移動について解説しました。
平行移動・・・図形をある方向に一定の長さだけずらす移動
回転移動・・・図形をある点を中心にとして、一定の角度だけ回す移動
対称移動・・・図形をある直線\(l\)を軸にして裏返す移動
「イマイチよく分からない…」という子はこちらの動画を見てみてください!とても分かりやすいです!






コメント