こんにちは!ケントです!
今回は正の数と負の数について詳しく解説します!
自然数や整数との違いなども分かりやすく解説しています!
反対向きの性質をもつ数①

反対向きの性質をもつ数とは何なのでしょうか?
天気予報などで「最低気温は氷点下3℃です」という言葉を一度は聞いたことがあると思います。
この「氷点下」は言い換えると「0℃よりも低い」という意味です。
温度計を想像してください。
3℃は0よりも3目盛分だけ上にあります。氷点下3℃は0よりも3目盛分だけ下にあります。
これらを区別するために0よりも上にある3℃を「プラス3℃」、0よりも下にある3℃を「マイナス3℃」と表現します。
反対向きの性質をもつ数はある基準を定めてその基準を0とし一方を+を使って表すと、もう一方は-(マイナス)を使って表すことができます。
+とーは互いに反対向きです。
このように、世の中には反対向きの性質をもつ数、すなわち+とーで表される数がたくさんあります。先ほど例に挙げた「温度」もその一つです。
小学校までは+の数のみを考えてきました。中学校ではーの数も考えることになります。
高さを+と➖で表そう
「高さ」についても日本一高い山の富士山の高さを+3776mと表すと、世界一深い海溝のマリアナ海溝は-10920mと表すことができます。
向きを+と➖で表そう
次に、「向き(方向)」について考えてみましょう。
東西に通じる道路上でどちらにも進まないことを基準の0とします。
東へ2km進むことを+2kmと表現すると、西へ5km進むことはどのように表されるでしょうか?
東に進むことを+と決めているので、東の反対向きである西に進むことは-で表せます。
西に5km進むことはー5kmと表せますね。
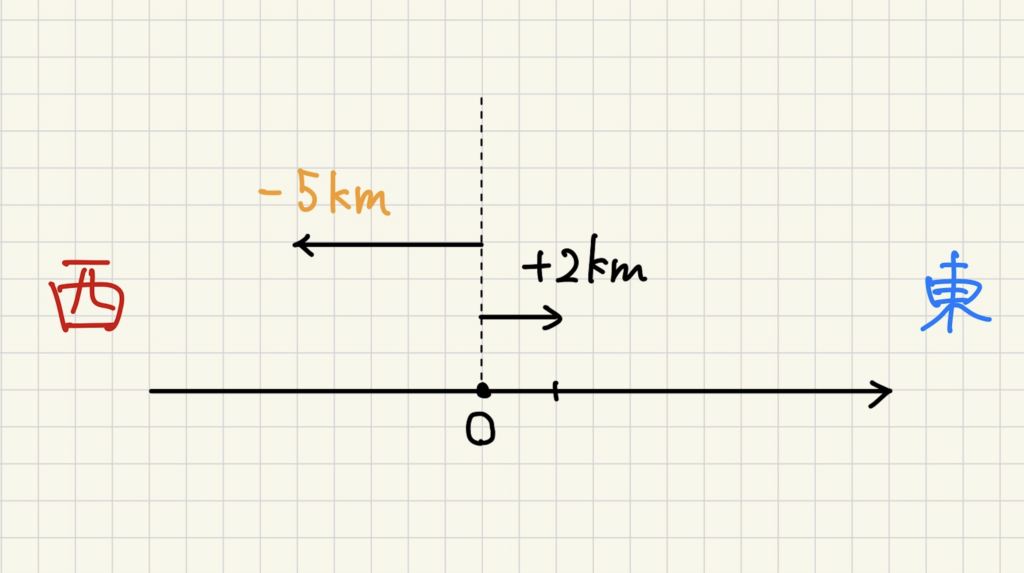
ここで注意したいのが、+の向きを勝手に東と決めたことです。
西に進むことを+としたら、東に2km進むことはー2kmと表されます。
大事なことは、どちらの向きを+にするかです。
+の向きが変われば、表し方も変わることを覚えておきましょう。
反対向きの性質をもつ数②
東西の道を進むとき、一方を+と表現すると、もう一方はーと表されることを学びました。
+とーが何度も出てきて、混乱している人もいると思います。
他の例をもとに話を整理しましょう。
「4cm短い」をー(マイナス)を使って言い換えるとどのようになるでしょうか?
日本語の問題です。
とりあえず4cmにーをつけると、ー4cmとなります。
「ー4cm短い」とすると、4cm長いことになってしまいますよね。
なので「短い」を「長い」に変えてあげればいいのです。
「4cm短い」をーを使って言い換えると「ー4cm長い」と表現できます。
同じように、
「2個増える」をー(マイナス)を使って言い換えるとどのようになるでしょうか?
ー2個とすると「増える」を「減る」に変えてあげれば2個増えることになります。
よって、「2個増える」をーを使って言い換えると「ー2個減る」と表現できます。
+とーの感覚を身につけるために、ここで演習問題をやってみましょう。
次の①〜③をー(マイナス)を使って表しなさい。
①5年前 ②階段を7段上がる ③300円の支出
正の数と負の数
0よりも大きい数を正の数、0よりも小さい数を負の数と言います。
正の数は+(プラス)の記号を使い+1、+10のように表し
負の数はー(マイナス)の記号を使ってー1、ー10のように表します。
普通は+は省略して書くことが多いですがーは省略できません。
ここで注意しなければならないのが
0は正の数でも負の数でもない
ということです。
意外とこれを忘れている子が多いので注意してください!
ここまでの説明を図でまとめました↓
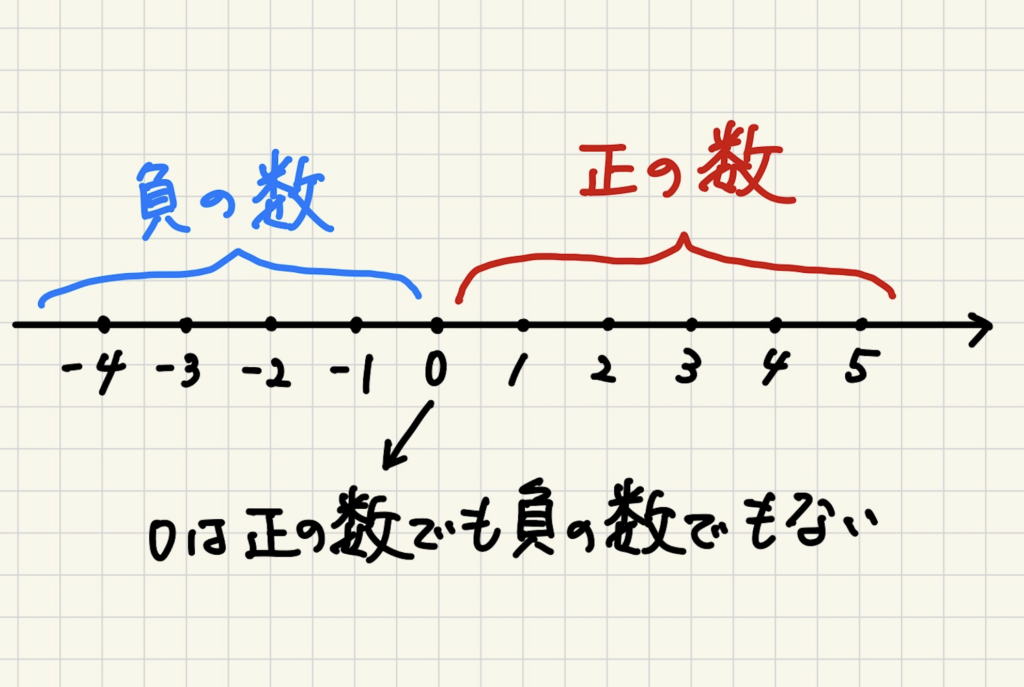
この図を見ると分かるように、負の数は「0よりも○小さい数」と表現できます。
具体的に、「ー2」は「0よりも2小さい数」と表現できますし、「ー10」は「0よりも10小さい数」と表現できます。
小学校までの算数では「1ー5=?」のような引き算はしませんでした。
負の数を知らなかったからです。
これからの数学では答えが負の数になる引き算も登場します!
絶対値
先ほどの図のように、数を数直線で考えることはとても大事なことです。
中には数直線に苦手意識がある人もいるかもしれませんが数直線はとても重要なので、ここで復習しましょう。
まず、数直線を考えるときに知っておかなければならない語句があります。
下の図を見てください。↓
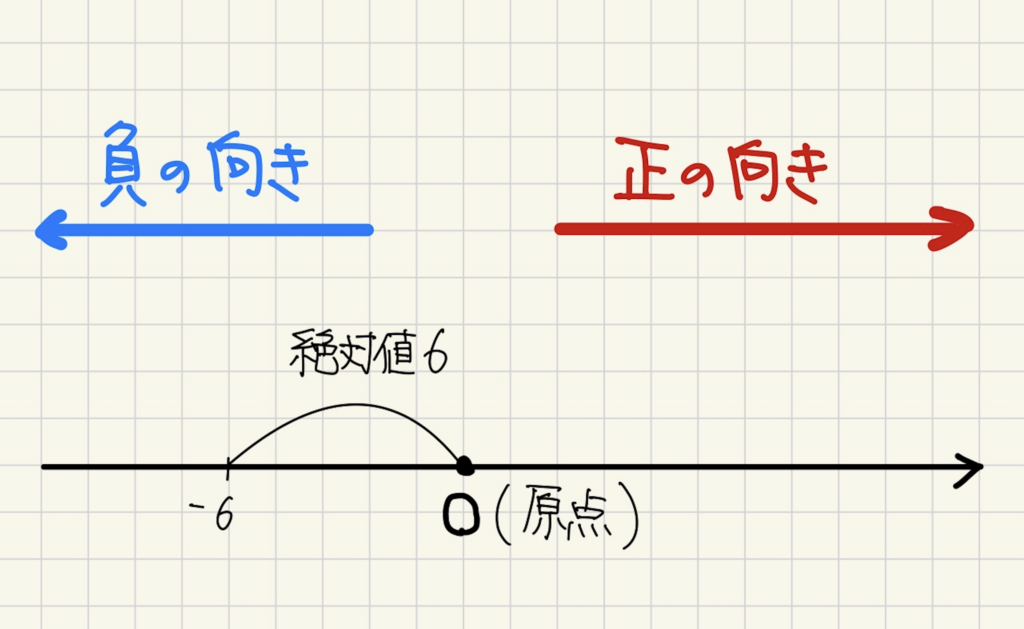
0の位置を原点(げんてん)と言い、アルファベットのO(オー)で表します。
また、数直線の左から右への向きを正の向きこれと反対向きを負の向きと言います。
0(原点)からある数までの距離(長さ)を絶対値と言います。例えば、3までの絶対値は3であり、ー3までの絶対値も3になります。
絶対値はゼロからの距離のことなので、+やーは関係ありません。
0の絶対値は0です。
問: −4の絶対値は? 答え: 4
簡単ですね。でもこの問が逆になると間違える人が続出します。
問: 絶対値が4の数は? 答え: 4と−4
0以外の数には、絶対値が同じ数は2つあります。
そうです、+と-の2つです!
数の大小を表そう
数の大小を比較するときは、不等号と言われる<(小なり)や>(大なり)といった記号を使います。
A<Bと書くとAよりもBの方が大きく
A>Bと書くとBよりもAの方が大きいという意味になります。
具体的に、-3<0, 5>-1, 3<4 のように使います。
ではここで、数直線についての演習問題をやってみましょう。
次の①〜③の問いに答えなさい。
①5と-3を表す点を数直線上にかきなさい。
②絶対値が5である数をすべて答えなさい。
③絶対値が3より小さい数をすべて答えなさい。
まとめ
・正の数は0より大きく、負の数は0よりも小さい
・0は正の数でも負の数でもない
・正の数は絶対値が大きいほど大きい
・負の数は絶対値が大きいほど小さい




コメント