こんにちは!ケントです!
今回は中学数学の4つ目の単元である「比例・反比例」の最初の内容です。
ここでは関数の基礎について解説していきます!
関数とは?
次のように「関数」は定められています。
\(x\)の値を決めると、それに対応して\(y\)の値がただ1つに決まるとき\(y\)は\(x\)の関数である。
たとえば、正方形の1辺の長さを6cmと決めると
正方形の面積は6×6=36で36cm2と決まります。
また、正方形の周の長さは6×4=24で24cmと決まります。
正方形の1辺の長さを決めると正方形の面積や正方形の周の長さは36cm2や24cmとただ1つに決まります。
すなわち、正方形の面積と正方形の周の長さは正方形の1辺の長さの長さの関数と言えるのです。
関数とは言えないもの
では「体重は身長の関数である」は正しいでしょうか?
答えは正しくないです。
たしかに、身長が高くなれば、それに伴って体重も大きくなりそうです。
しかし、身長を160cmと決めても体重はただ1つに決まりません。
身長160cmで40kgの子もいれば、身長160cmで50kgの子もいます。
体重と身長には関係はありそうですが、身長を決めても体重がただ1つに決まらないので関数とは言えないのです。
大事なことは、\(x\)を決めたときに、\(y\)の値がただ1つに決まるかどうかです。
「ただ1つに」という部分が重要でテストでもよく出題されます!
それでは、ここで確認問題をやってみましょう!
次の①〜④のうち、関数と言えるものをすべて選びなさい。
① 1個\(x\)円のみかんを10個買うときの代金\(y\)円
② \(x\)時間のテスト勉強時間とそのテストの得点\(y\)点
③ 周の長さが\(x\)cmの正方形の面積\(y\)cm2
④ 年齢\(x\)歳の人の身長\(y\)cm
問題を考えてみよう
40Lまで入る水槽に毎分4Lで水を注ぐ。水を入れ始めてからの時間\(x\)分と水槽に入っている水の量\(y\)Lとするとき、\(x\)と\(y\)の関係を考えます。
関数の問題を考えるときは表やグラフを作成すると考えやすいです。
表を完成させると下のようになります!↓
| \(x\)(分) | 1 | 2 | 3 | 4 | ・・・ | 10 |
| \(y\)(L) | 4 | 8 | 12 | 16 | ・・・ | 40 |
次は、グラフをかいてみます。
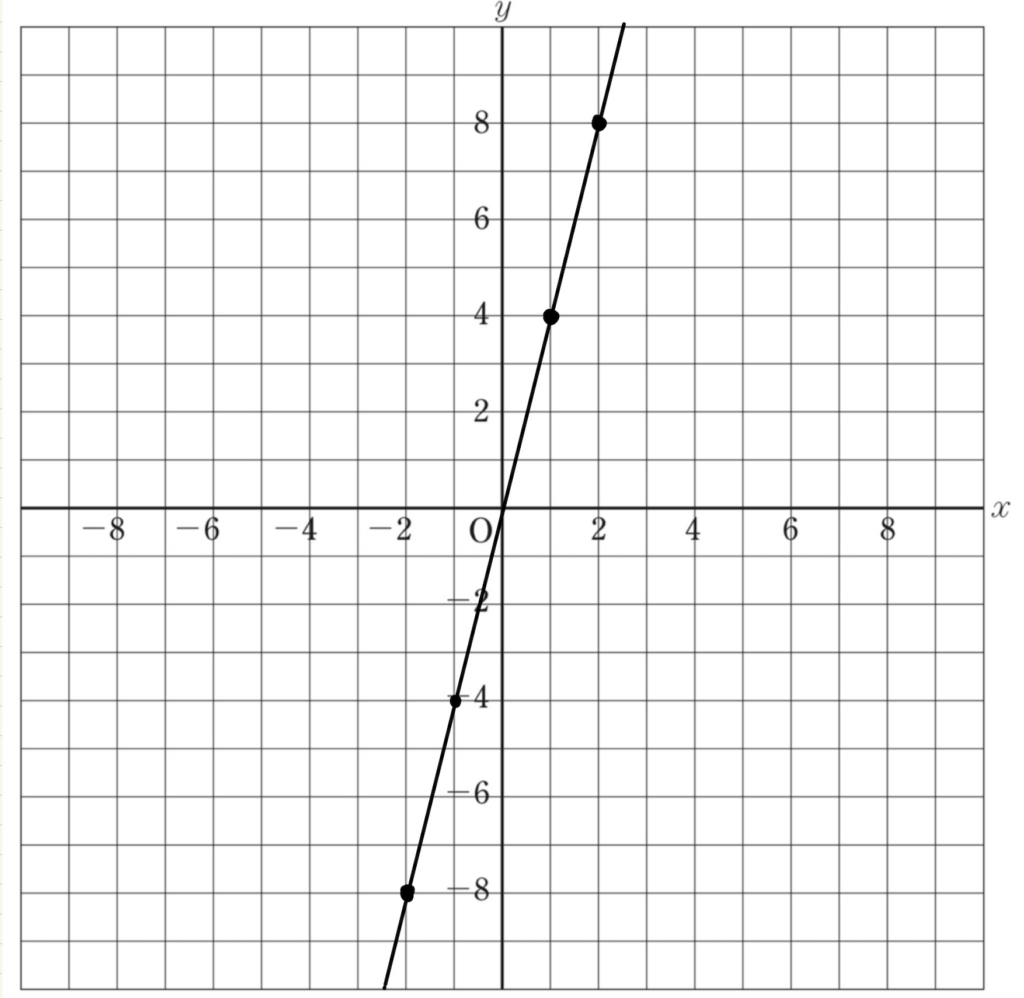
また、\(y\)を\(x\)で表すと\(y=4x\)となります。
数量を文字で表すことに苦手意識がある子は以下の記事をチェック!
今回、水槽は40Lまでしか入らないので、10分で満タンになることが分かります。
変数と変域
\(y\)や\(x\)のようにいろいろな値を取ることができる文字を変数と言います。
また、この問題では10分で水槽が満タンになるので水を入れ始めてからの時間は0分〜10分までしか考えられません。
このように\(x\)や\(y\)の取りうる値の範囲を変域(へんいき)と言います。
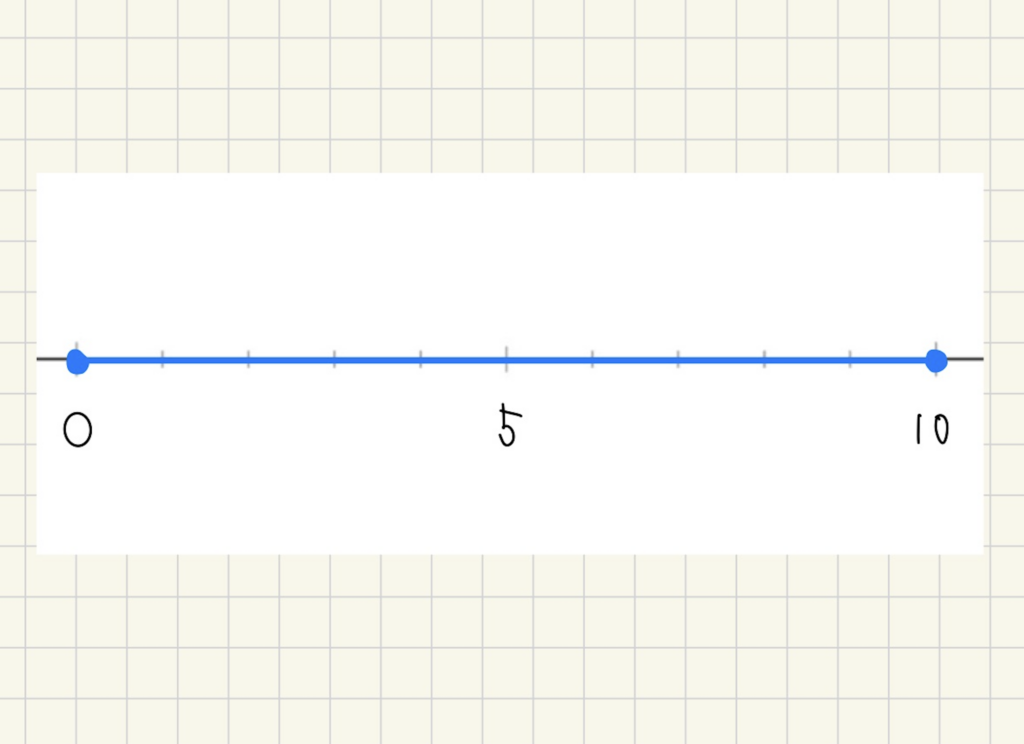
今回の問題の変域を不等号で表すと
0≦\(x\)≦10となります。
不等号(<や>)が分からない子は以下の記事をチェック!
さらに、0≦\(x\)≦10を数直線で表すと下の図のようになります!↓
まとめ
関数の基礎となる考え方や重要語句をまとめました!
忘れないようにノートにメモをしておきましょう。
【まとめ】
① 関数とは\(x\)を決めると、それにともなって\(y\)もただ1つに決まるもの。
② 関数の問題は表やグラフをかくと良い。
③ 色々な値を取ることができる文字を変数、
取りうる値の範囲を変域と言う。





コメント