比例と比例定数

こんにちは！ケントです！

今回は小学校でも勉強した比例について、その特徴や考え方、テストでよく出るところを解説していきます！

比例は関数の1つです。

関数ってなんだっけ？という子は以下の記事をチェックしてみてください！

比例とは何か？

下の図のような、東西に伸びる道を想像してください。

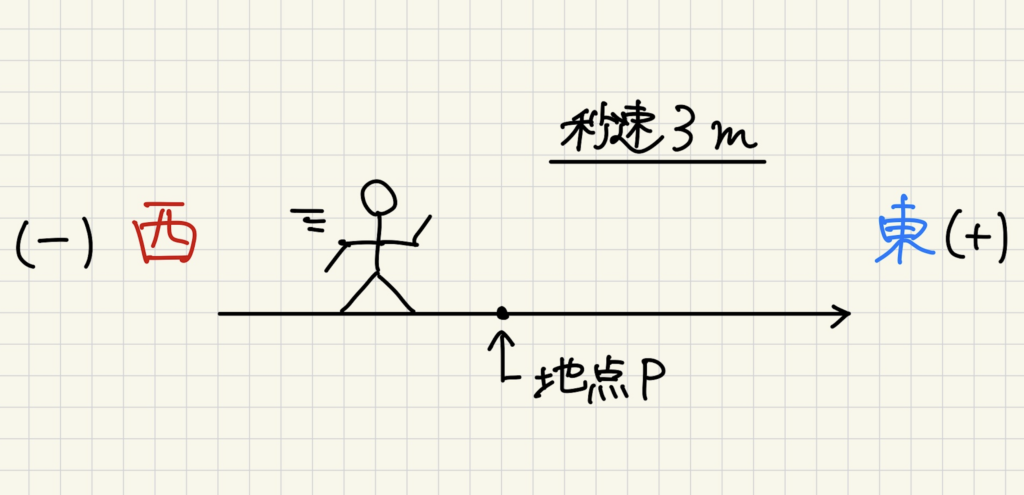
Aさんは秒速3mで西から東に向かって走っています。

Aさんが地点Pを通過してからの時間を\(x\)、Aさんがいる位置を\(y\)とします。

すると、Aさんの走っている様子は下の表のように整理されます。

\(x\)(秒)	-3	-2	-1	0	1	2	3
\(y\)(m)	-9	-6	-3	0	3	6	9

ここで、正負の数を考えると「－3秒」は「3秒前」、「－9m」は「地点Pから西に9m」と読み替えることができますね。

正負の数について復習したい子は以下の記事をチェック！

つまり、Aさんは3秒前には地点Pから西に9m進んだ地点にいたということです。

では、\(x\)と\(y\)の関係を式で表してみましょう！

\(x\)が1,2,3…と増えると
\(y\)は3,6,9…と増えるので
\(y=3x\)と表すことができますね！

数量を式で表すことが苦手な子は以下の記事をチェック！

\(y=3x\)のように

比例の特徴①

\(y=ax\)と表されるとき、\(y\)は\(x\)に比例すると言います。

比例についてその性質や特徴などを説明していきます！

これは定期テストでも頻出の内容です。

先ほどの表を見てみましょう。

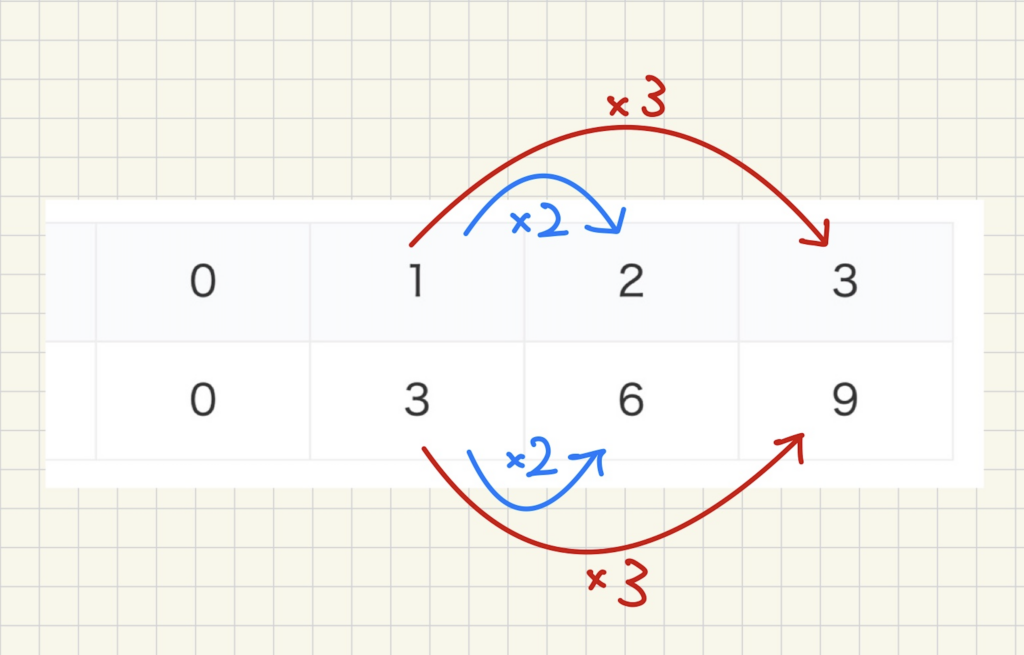
\(x\)が1から2に2倍されると
\(y\)も3から6に2倍されています。

\(x\)が1から3に3倍されると
\(y\)も3から9に3倍されています。

\(x\)も\(y\)も同じように増加していくということです！

比例の特徴②

続いて、比例の特徴の2つ目です！

先ほどの表を見てください。

\(\frac{y}{x}\)の値、すなわち\(y\)を\(x\)で割った値は常に3になっているはずです。

比例定数は\(y÷x\)で求められるということです！

比例の特徴③

続いて、比例の特徴の3つ目です。

先ほどの秒速3mで走るAさんの式\(y=3x\)をグラフにすると下の図のようになります。↓

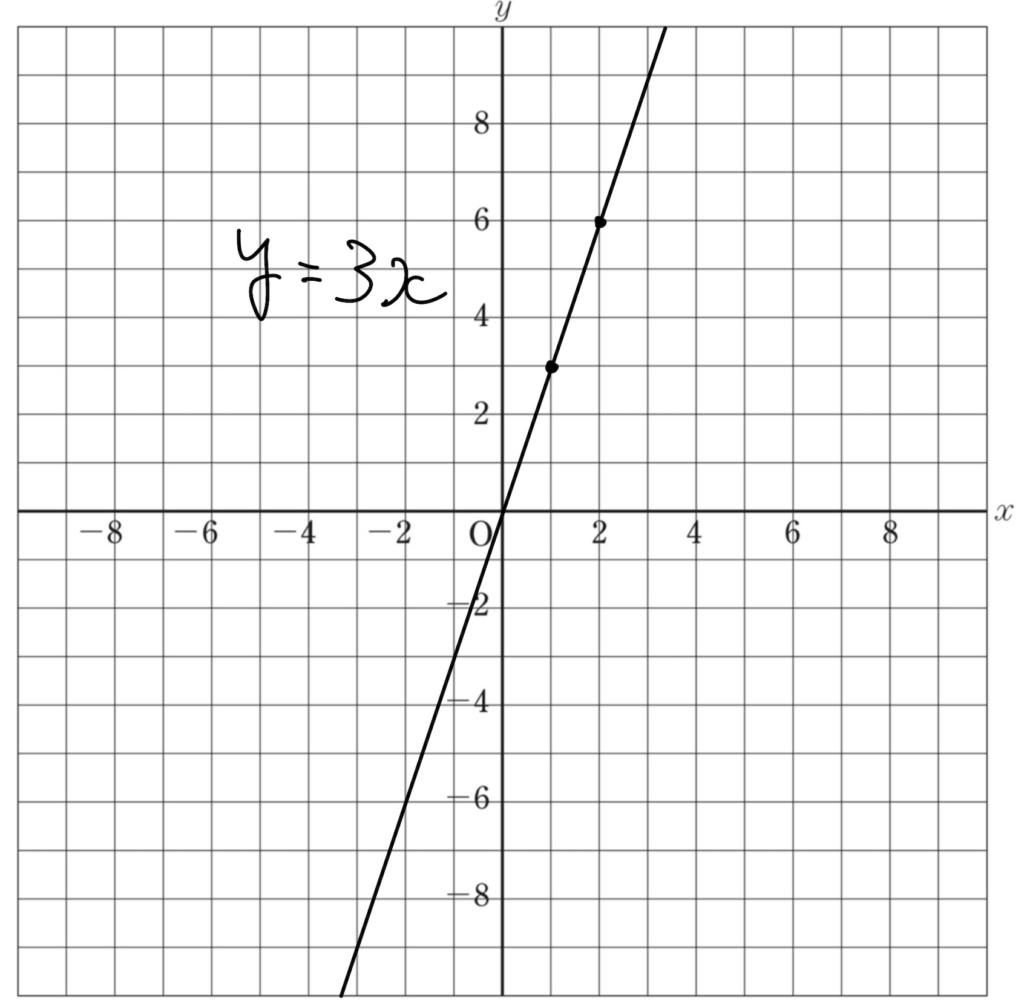
原点Oを通る直線になっていますね！

グラフは直線だけとは限らないので、「比例のグラフは直線」という理解はとても大切です。

比例定数が負の場合

\(y=ax\)で表されるとき\(y\)は\(x\)に比例すると言います。また、\(a\)を比例定数と言います。

では比例定数が負の場合はどうなるのでしょうか？

試しに\(y=-2x\)の比例を考えてみましょう。

\(x\)	-3	-2	-1	0	1	2	3
\(y\)	6	4	2	0	-2	-4	-6

\(y=-2x\)の表はこのようになりました！

比例の特徴①について
\(x\)が1から2に2倍されると
\(y\)も-2から-4に2倍されています。

また、比例の特徴②について、\(\frac{y}{x}\)の値は常に－2で一定です。

さらに、＜比例の特徴③＞についてグラフは下のようになります。↓

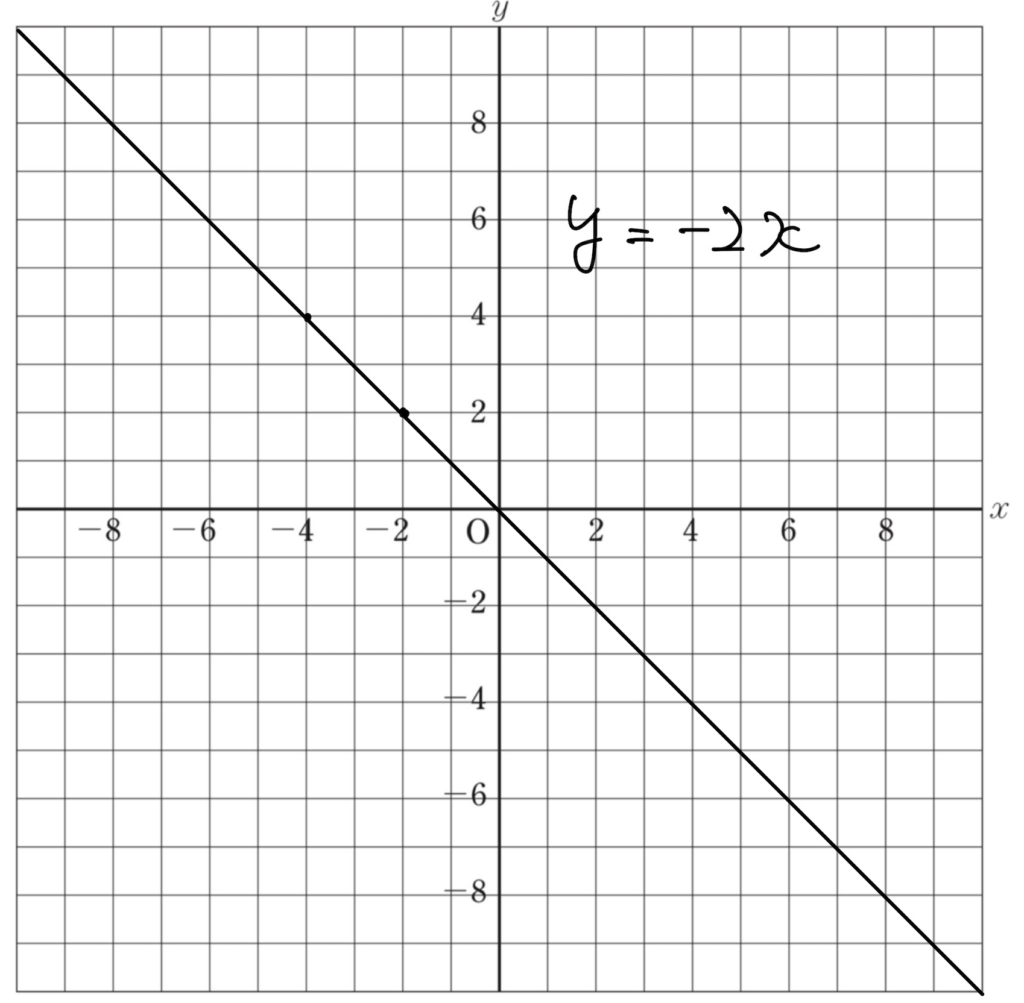
原点を通る直線になっていますね！

比例定数が負の数の場合でも3つの特徴はすべて当てはまります！

これからは比例定数が負の場合も当然のように扱っていきます。

ここでしっかりと特徴を覚えましょう！

まとめ

比例についてまとめました↓

\(y=ax\)で表されるとき\(y\)は\(x\)に比例すると言い、\(a\)を比例定数と言う。

＜特徴①＞\(x\)が1倍,2倍…となると、\(y\)も1倍,2倍…となる
＜特徴②＞\(\frac{y}{x}\)の値は比例定数に等しい
＜特徴③＞グラフは原点を通る直線になる