点と直線

こんにちは！ケントです！

中1単元「平面の図形」の最初の内容です。

今回は点と直線について詳しく解説していきます！

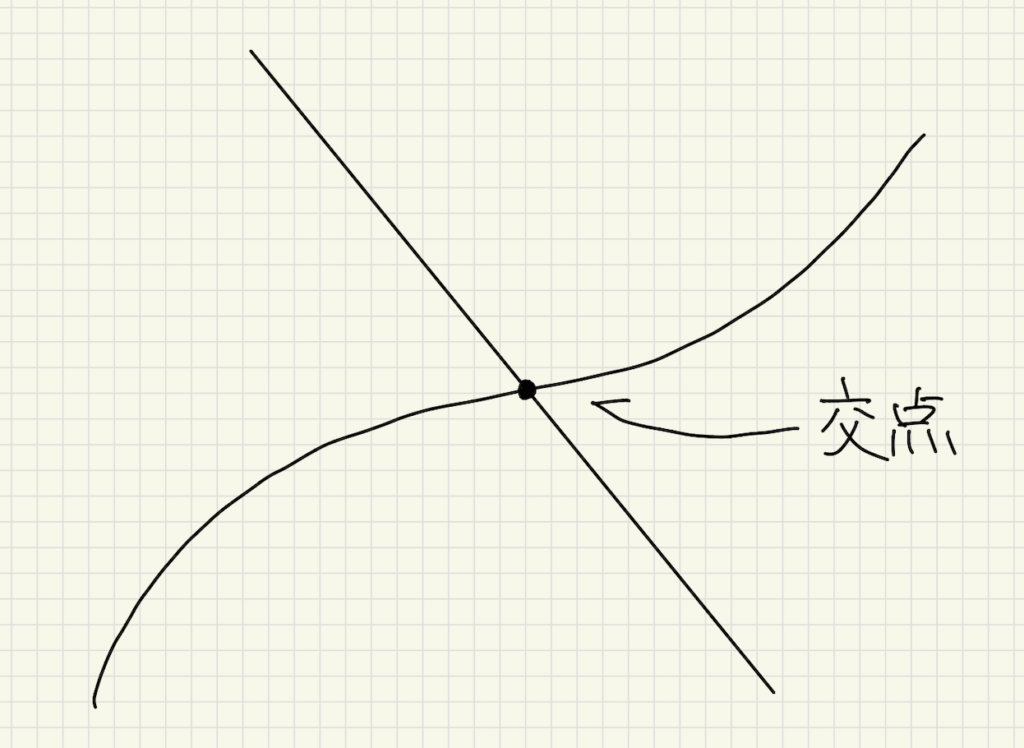
交点とは？

下の図のように線と線が交わる部分を交点と言います。

直線、半直線、線分の違い

これまで、何となく「直線」と言ったり、「線分」と言ったりしてきました。しかし、厳密には直線と線分は少し違います。また、新しく半直線というものも登場します。それらの違いについて解説します。

直線

直線・・・両方に限りなく伸びた線

教科書に両方に限りなく伸びた線をかくと、めちゃくちゃになるので、実際には途中で止まっている線も直線と言われます。

半直線

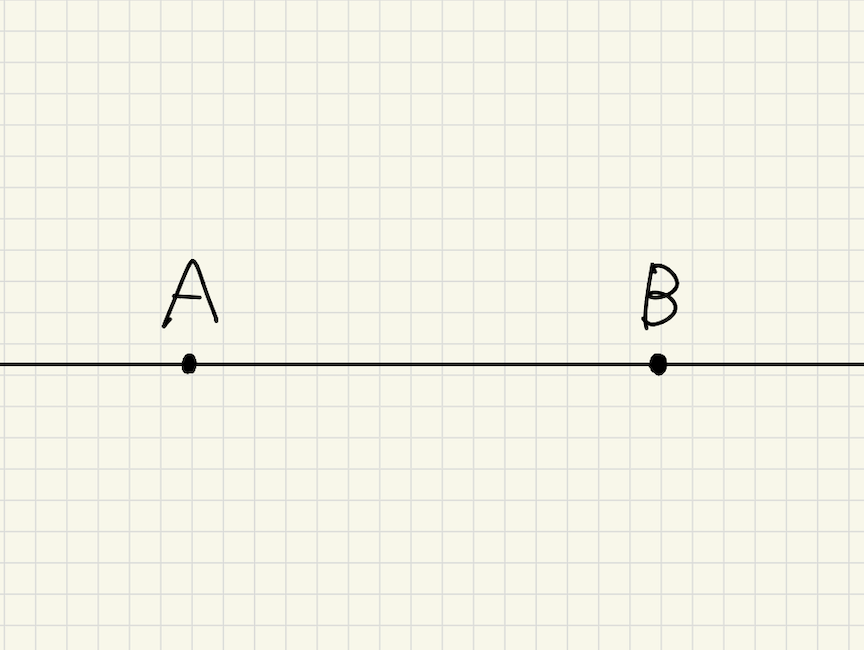
半直線・・・直線の一部で1点を端にして一方にだけ伸びた線

半直線ABの場合は「Aを端にしてBの方に伸びる」線

一方、半直線BAの場合は「Bを端にしてAの方に伸びる」線です。

※半直線の場合はABなのかBAなのか、アルファベットの順序が重要になります！

半直線AB

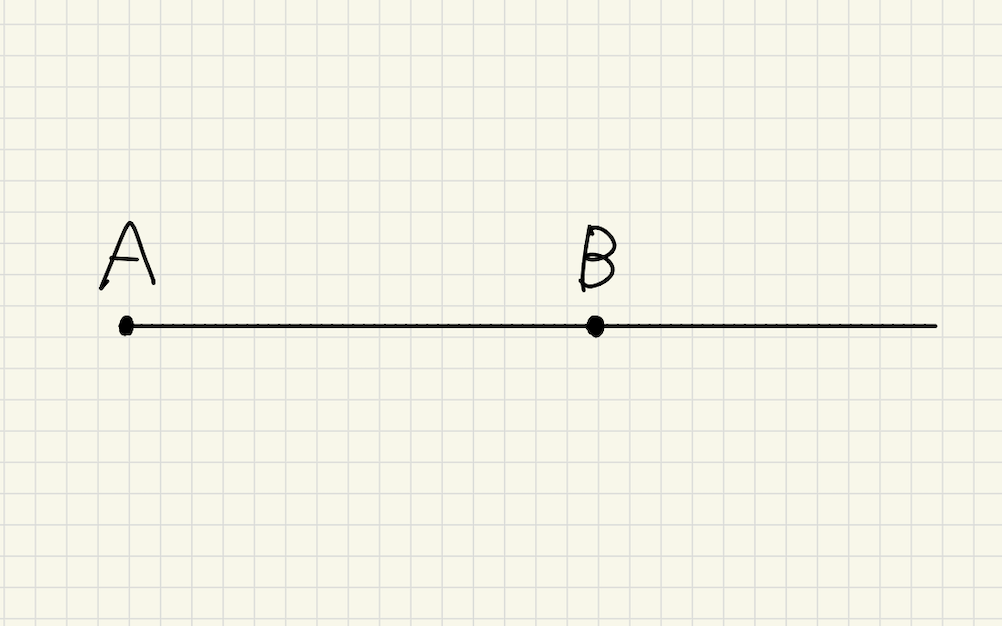
半直線BA

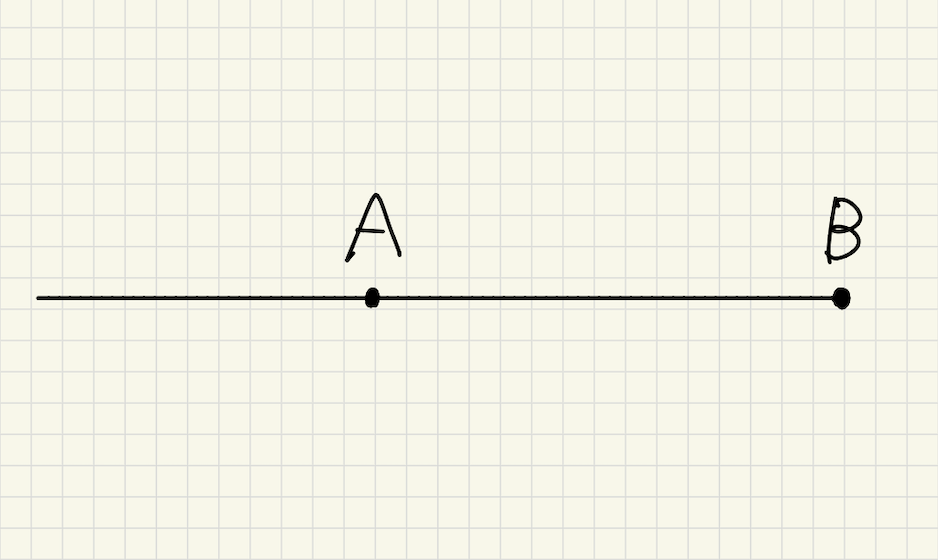
線分

線分・・・直線の一部で、2点を両端とする線

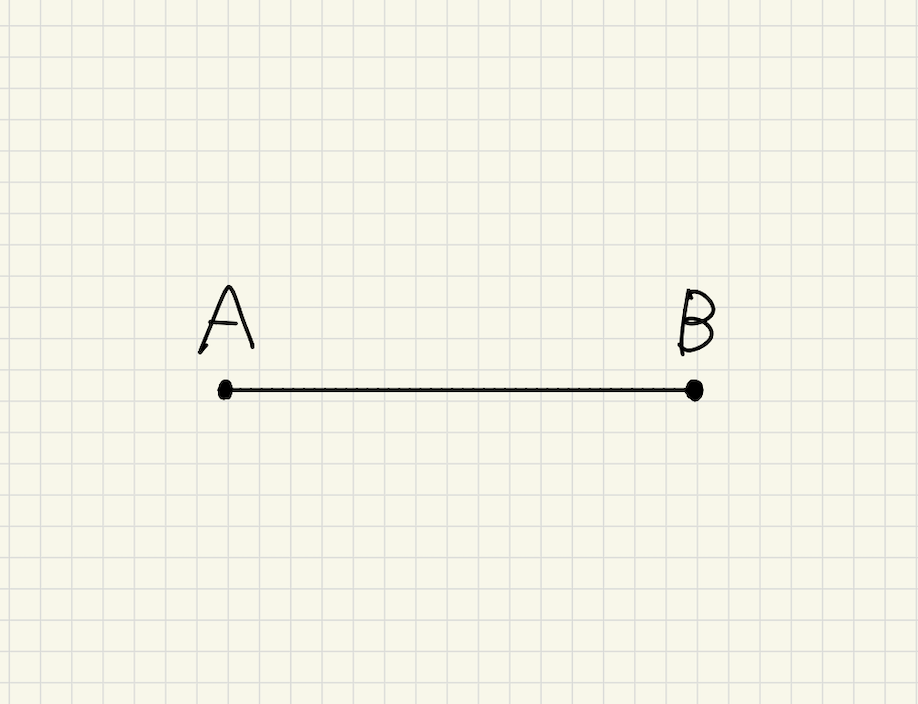
点と点の距離

下の図のように線分ABは点Aと点Bを結ぶ最も短い線です。

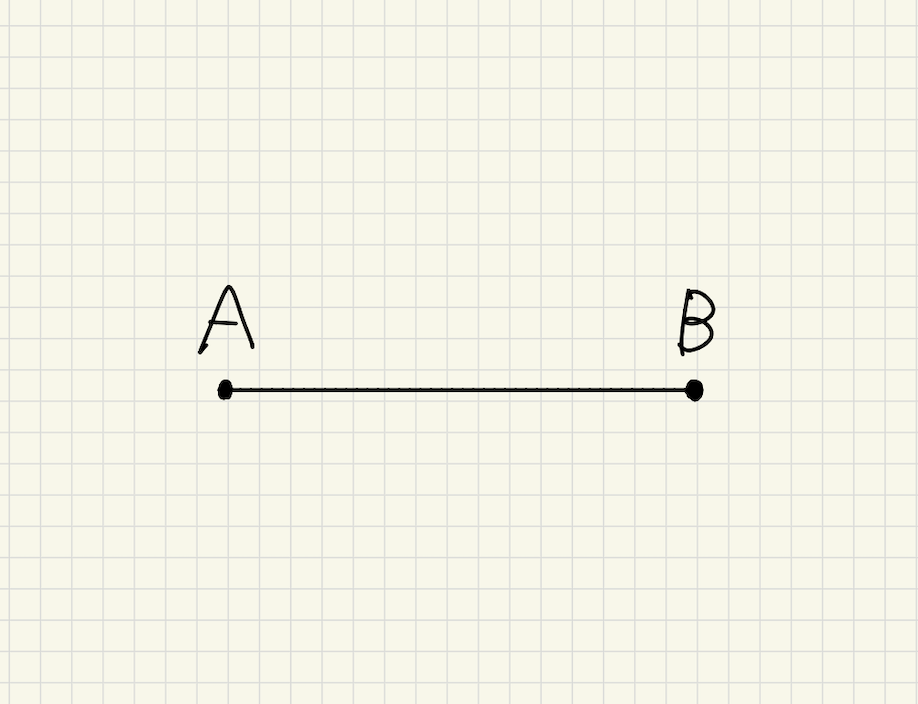
線分ABの長さを2点A,Bの距離と言い、ABと表します。

線分ABの長さが4cmのとき、AB＝4cmと書きます。

また、線分ABと線分CDが等しいとき、AB＝CDと書きます。

さらに、線分AB＝2cm，線分CD＝6cmのとき、線分CDは線分ABの3倍なのでCD＝3ABと表します。

使い方にもぜひ慣れていってくださいね！

直線がつくる角

下の図のような1点から引いた2本の半直線が作る図形が角です。

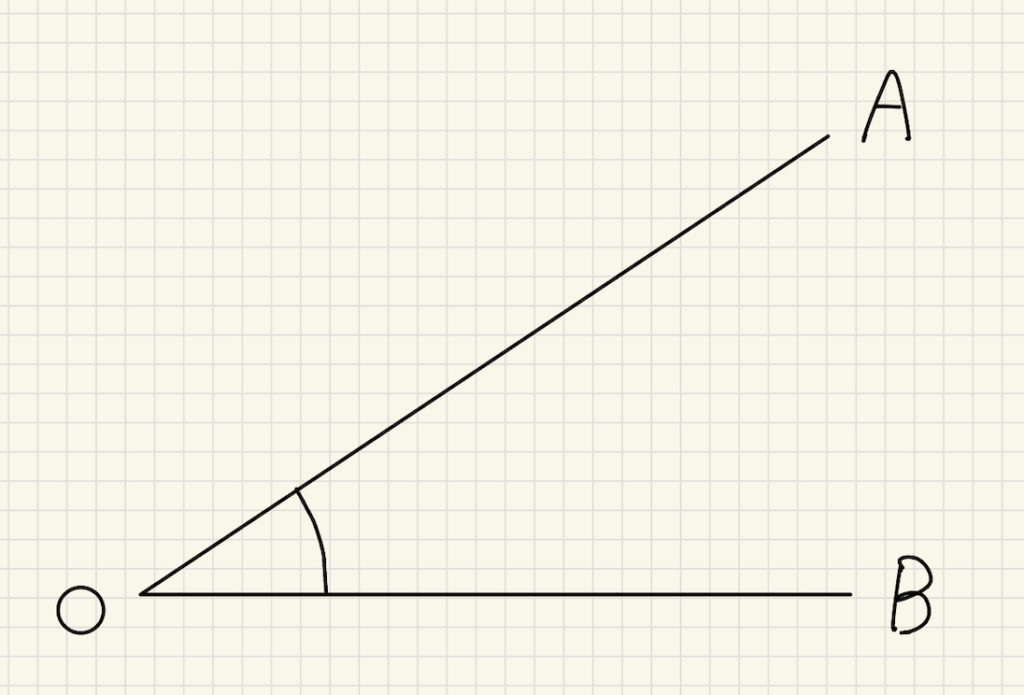
この角は∠AOBまたは∠BOAと表します。※角の先端部分を∠○○○の真ん中に書きます。

∠ABCの大きさが30°のとき、∠ABC＝30°と表します。

平面上の2直線

平面での2直線（2つの直線のこと）の関係を考えます。

下の図のように2直線は

①交わる場合
②交わらない場合

があります。当たり前のことのようですが大事なことです！

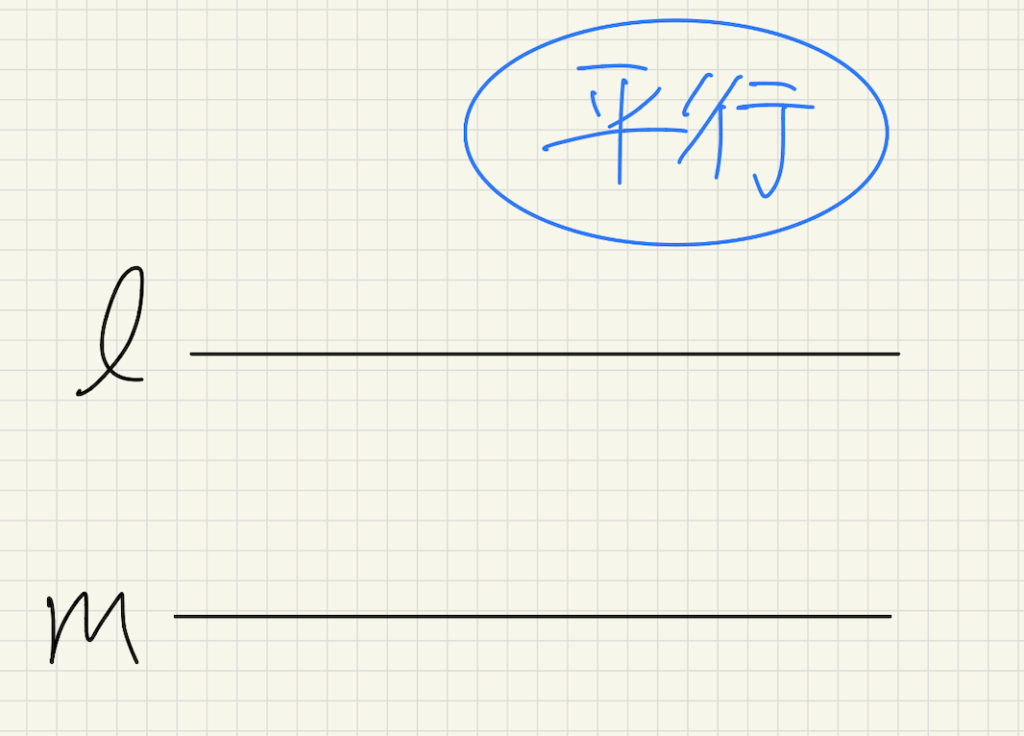
上の図のように、2直線\(l\)と\(m\)が交わらない場合、直線\(l\)と\(m\)は平行であると言います。

また、記号//を使って、\(l\)//\(m\)と表します。

下の図のように、2直線\(l\)と\(m\)が直角(90°)で交わる場合

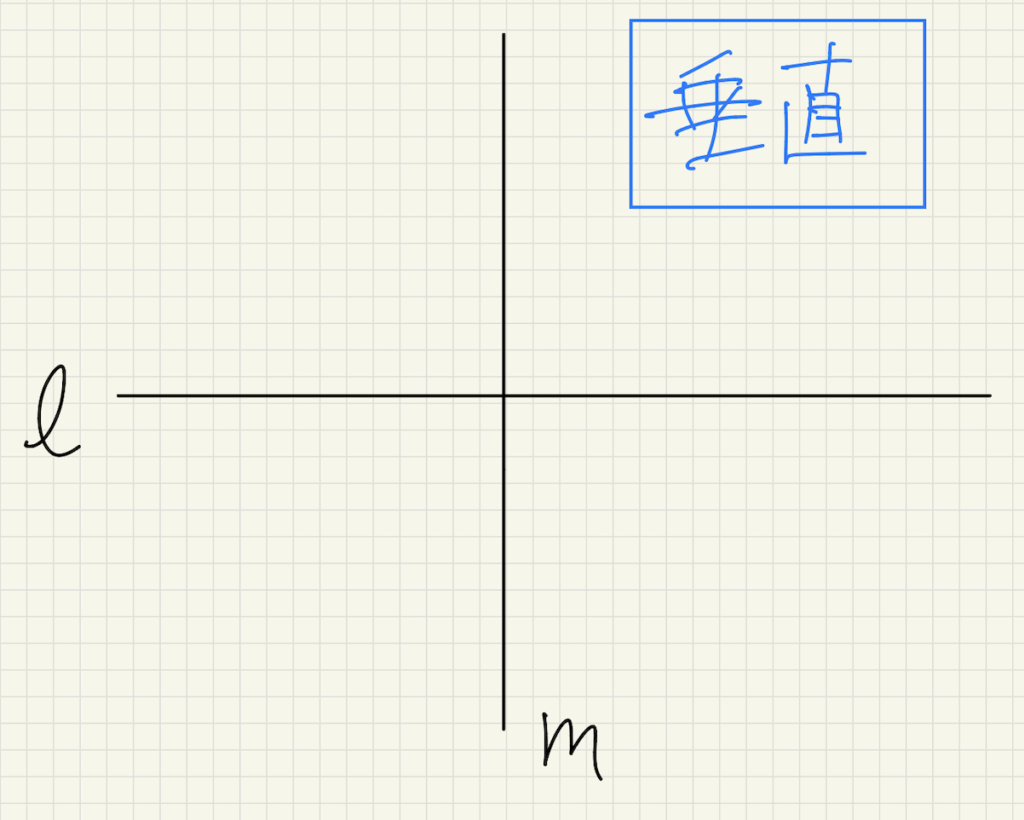
直線\(l\)と\(m\)は垂直であると言います。

また、記号\(\perp\)を用いて、\(l\)\(\perp\)\(m\)と表します。

さらに、直線\(l\)は直線\(m\)の垂線と言います。

距離

数学では「距離」という言葉をよく使います。

数学では、距離は最も短い線と覚えてください。

①点と点の距離

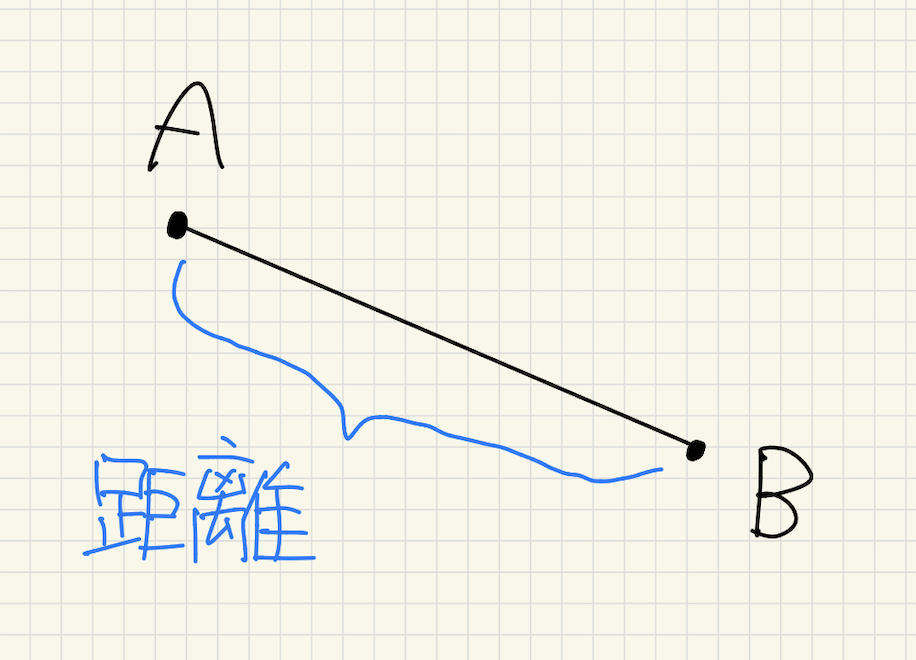
②点と直線の距離

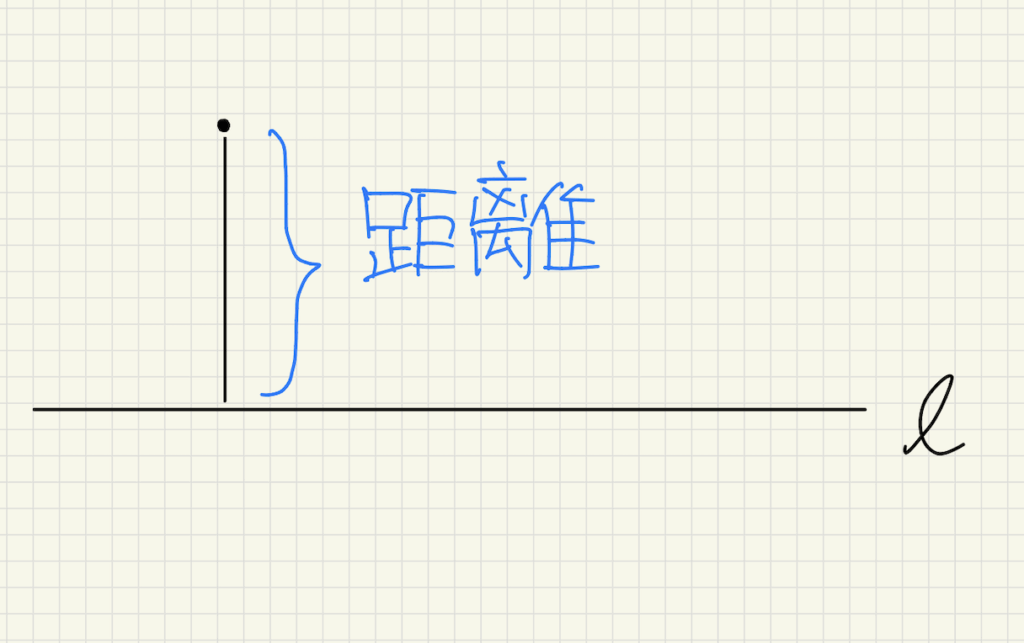
③直線と直線の距離

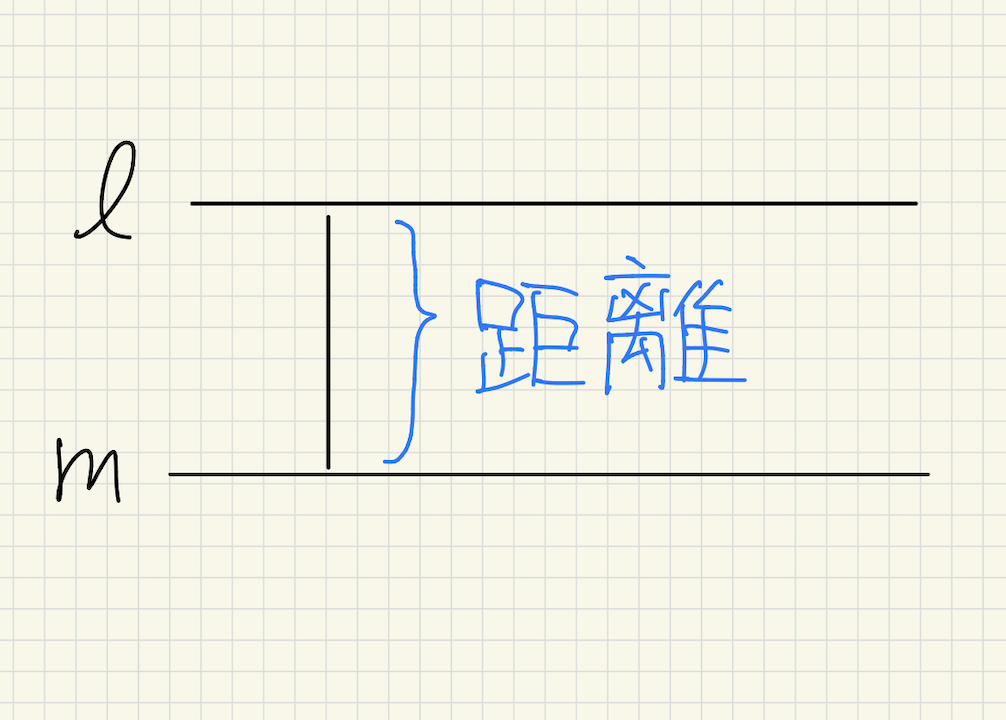
①点と点
②点と直線
③直線と直線
どれも結んだときに一番短くなる線が距離です！

何度も距離が出てきて混乱する子がいると思いますが最短の長さを数学では距離と言うことを覚えておいてください！

まとめ

点と直線についてまとめました！

【点と直線のまとめ】

直線：両方に限りなく伸びた線
半直線：直線の一部で、1点を端にして一方にだけ伸びた線
線分：直線の一部で、2点を両端とする線

直線\(l\)と\(m\)が平行　→　\(l\)//\(m\)
直線\(l\)と\(m\)が垂直　→　\(l\)\(\perp\)\(m\)