こんにちは!ケントです!
今回は円と扇形について分かりやすく解説していきます!
円とは?
「円は円だろ」と思う子もいるかもしれません笑
一応、数学的にはある1点から等しい距離にある点の集合が円であると決められています。
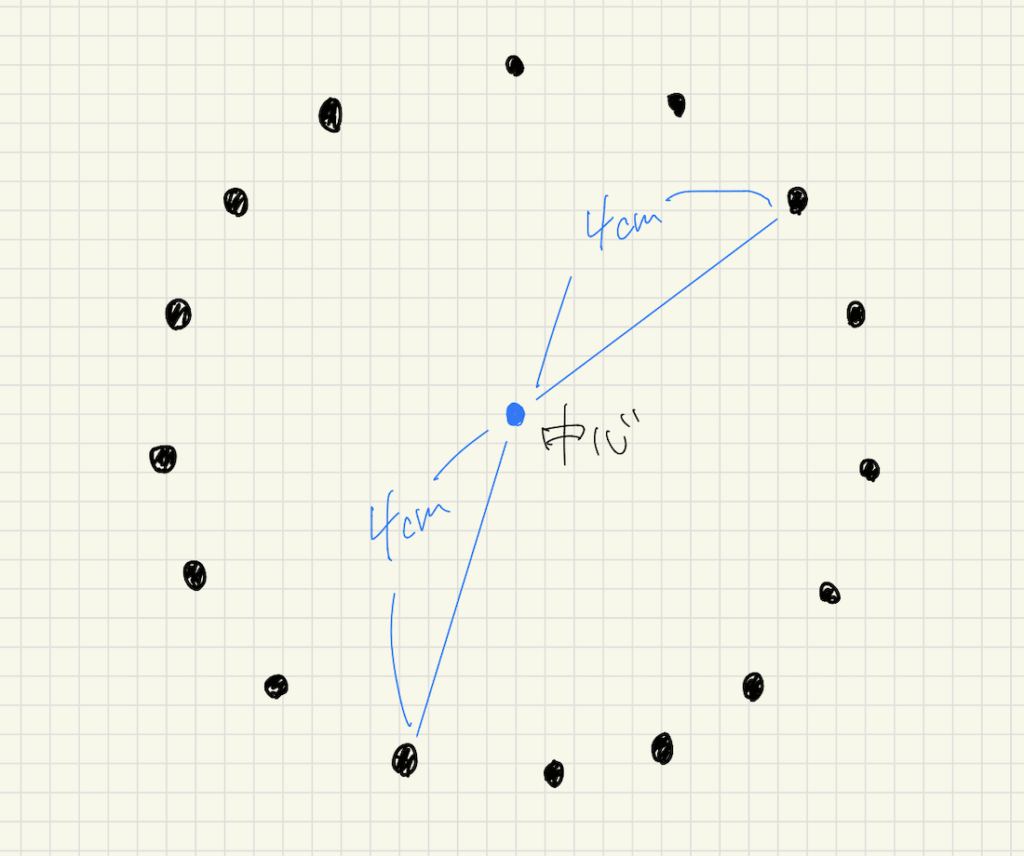
ある点を決めて、その点から4cmのところに点を取り続けたら、たしかに半径4cmの円ができますよね!
しかし、この説明は少し難しいので「円は円だ!」と覚えてもOKです。
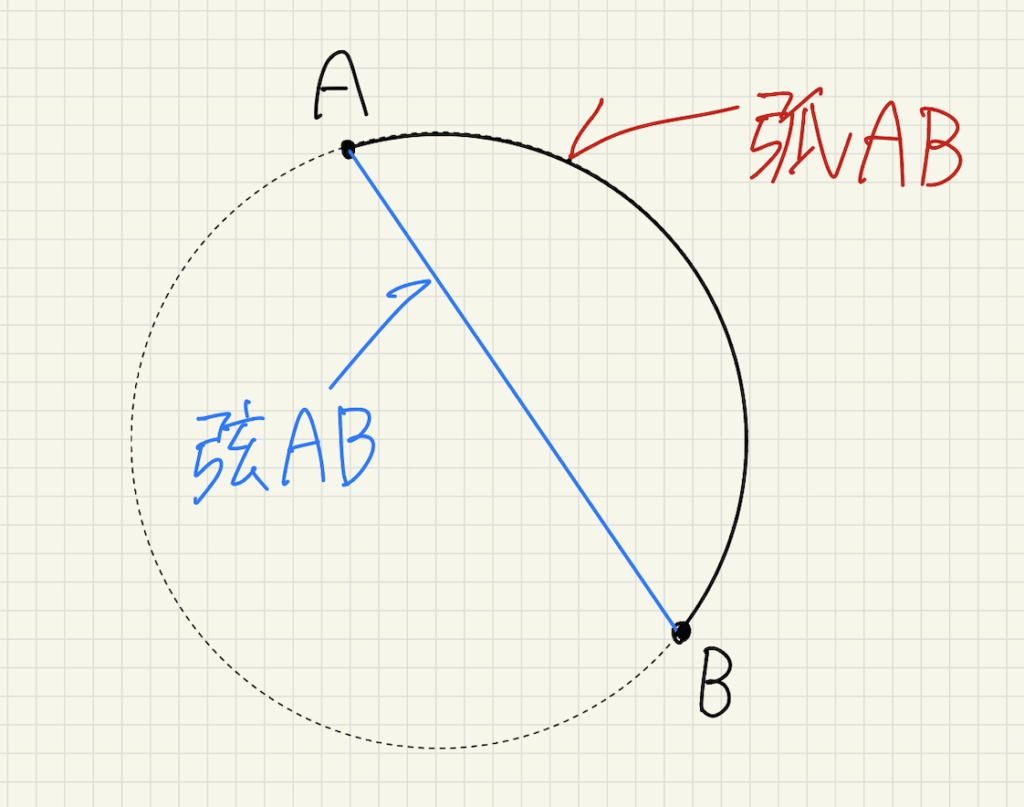
下の図で、円周の一部を孤(こ)と言います。円周上の点A,Bを両端にもつ孤を孤ABと言います。
また、円周上の点を結ぶ線分を弦(げん)と言います。点A,Bを両端とする弦を弦ABと言います。
接線と接点
下の図のように円が直線と1点で交わるとき、円と直線は接すると言います。
また、この直線を接線、交わる点を接点と言います。
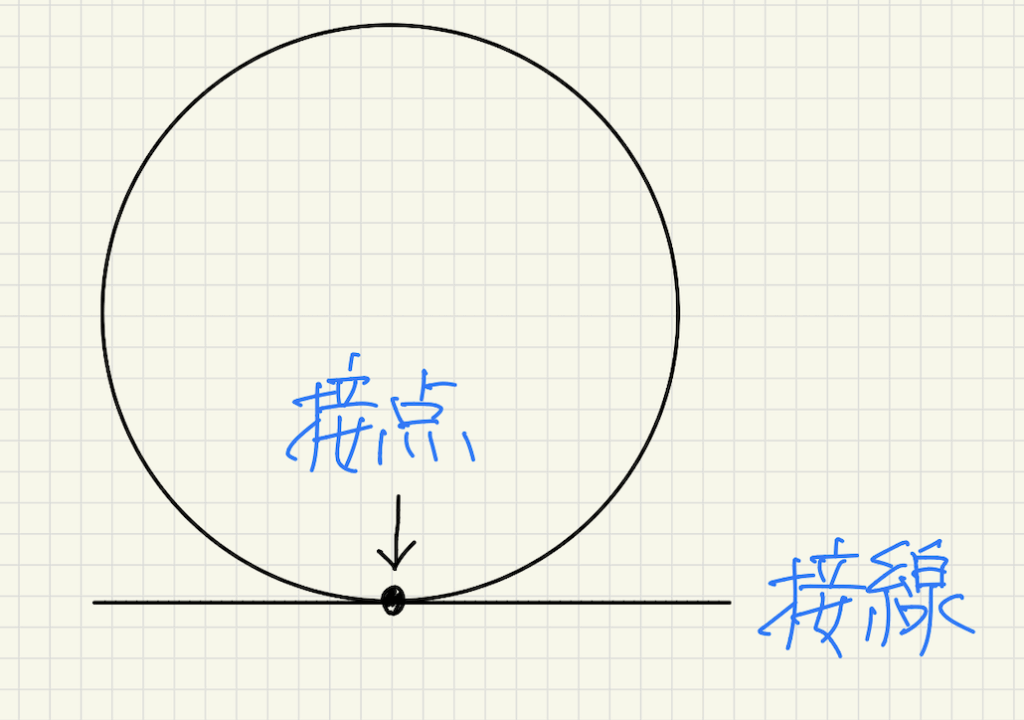
円の接線は半径と垂直に交わる
これは非常に重要な性質です。覚えておきましょう!
扇形とは?
扇は写真のような形の図形を指します。数学的には円の一部分が扇形です。
下の図で、∠AOBを孤ABに対する中心角と言います。
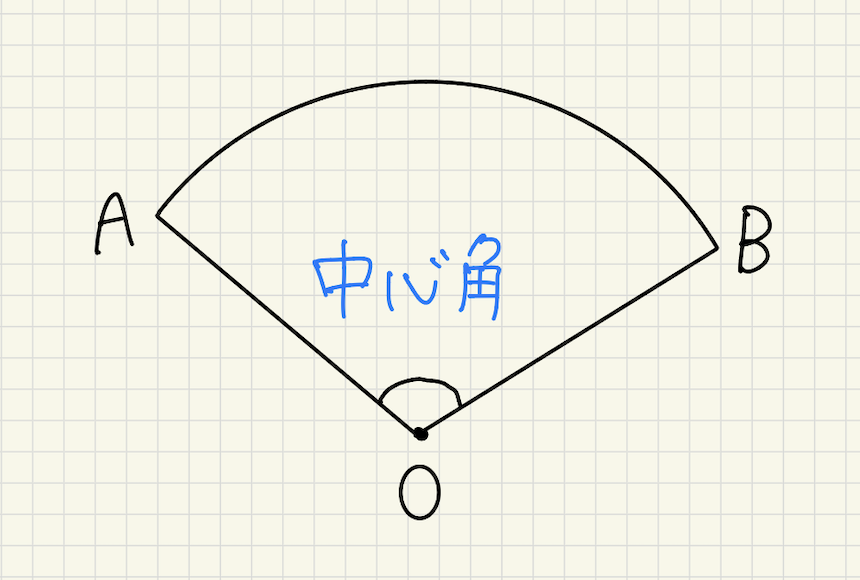
中心角が大きくなればなるほど、円に近い図形になっていきます。
円と扇形の面積
ここでは円と扇形の面積の求め方を紹介します!
円周の長さ:\(2πr\)
面積:\(πr^2\)
\(π\)は円周率3.14…です。
中学校では3.14の面倒な計算はしなくも良いです!\(π\)はそのまま残しておいてOKです。
円の公式は覚えてしまうのが早いですね。頑張って覚えましょう!
孤の長さ:\(2πr\times\frac{a}{360}\)
面積:\(πr^2\times\frac{a}{360}\)
※\(a\)は中心角
扇形の公式は覚えてしまってもいいですが、公式の意味をセットで理解しておくと忘れにくくなります!
扇形は円の一部です。円の中心角は360°ですね!
中心角が120°の扇形の場合、120°は360°の3分の1なので
この扇形の面積は、円の面積×\(\frac{1}{3}\)で求められます!
公式の\(\frac{a}{360}\)という部分は、この\(\frac{1}{3}\)の役割をしているのです。
ここで、演習問題をやってみましょう。
①〜③を求めなさい。扇形の中心角は60°とする。
①半径4の円の面積
②半径6の扇形の孤の長さ
③半径6の扇形の面積
まとめ
円と扇形についてまとめました!
【まとめ】
・円の接線は半径と垂直に交わる
・円の面積:\(πr^2\)
・扇形の面積:\(πr^2\times\frac{a}{360}\)




コメント